Codeforces Global Round 14 E

题目链接

https://codeforces.com/contest/1515/problem/E

题目截图

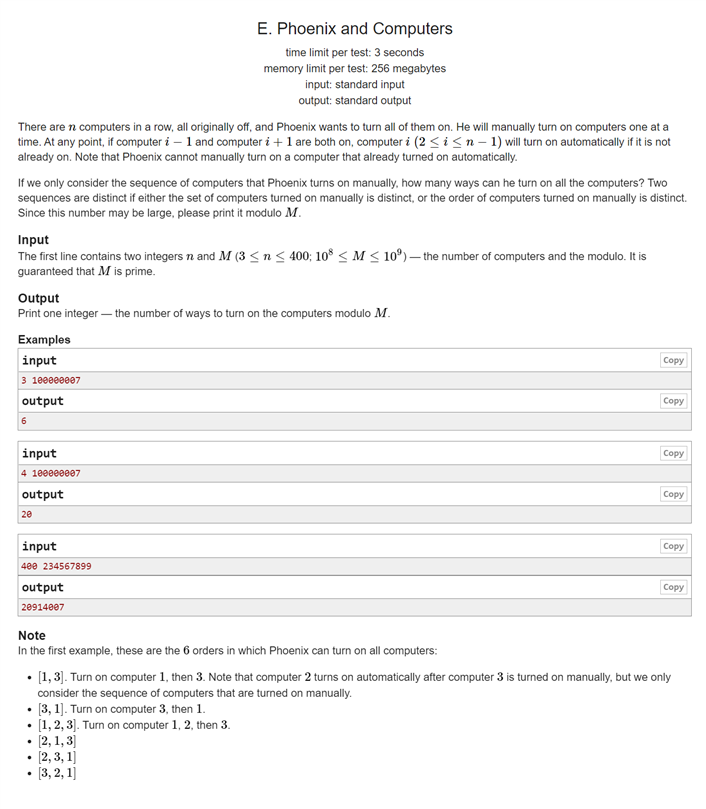
 题目大致描述

n台计算机初始均为关机状态，现欲将所有计算机均打开，一次只能手动打开一台，当打开第i - 1台和第i+1台且第i台未打开时，第i台会自动打开。
问：将所有计算机打开手动打开序列有多少种，结果对m取模

 题解

这题是一道线性dp题，难点主要在于状态转移方程中涉及到组合数学。

定义dp[i][j][k]表示前i个计算机有j个手动打开，且后缀有连续k台手动打开的方案数（模m）

之所以定义后缀，是因为可以证明只有连续的计算机的打开顺序是相互影响的

将k台放到j-k台中的情况有C(j, k)种（不考虑顺序），而连续k台的排列有2^k-1 种情形

则转移方程有

dp[i][j][0] = Σdp[i-1][j][0] 

dp[i][j][k] = dp[i-k][j-k][0] × C(j, k) × 2^k-1

#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define IOS std::ios_base::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
using namespace std;
using ll = long long;
const int maxn = 401;

int n;
ll mod;
int jie[maxn], p_pow[maxn], c[maxn][maxn];
int dp[maxn][maxn][maxn];//i, zongong, houzhui

inline void pre_do() {
	jie[0] = p_pow[0] = 1;
	for(int i = 1;i <= n;++i) {
		jie[i] = ll(jie[i-1]) * i % mod;
		p_pow[i] = ll(p_pow[i-1]) * 2 % mod;
	} 
	for(int i = 1;i <= n;++i) {
		c[i][0] = c[0][i] = 1;
	}
	for(int i = 1;i <= n;++i) {
		for(int j = 1;j <= n;++j) {
			c[i][j] = (ll(c[i-1][j]) + c[i][j-1]) % mod;
		}
	}
}

inline void solve() {
	dp[0][0][0] = 1;
	for(int i = 1;i <= n;++i) {
		for(int j = 1;j <= i;++j) {
			for(int k = 1;k <= j;++k) {
				dp[i][j][0] = (ll(dp[i][j][0]) + dp[i-1][j][k]) % mod;
			}
			for(int k = 1;k <= j;++k) {
				dp[i][j][k] = ll(dp[i-k][j-k][0]) * c[j-k][k] % mod * p_pow[k-1] % mod;
			}
		}
	}
	ll ans = 0;
	for(int i = 1;i <= n;++i) {
		for(int j = 1;j <= i;++j) {
			ans = (ans + dp[n][i][j]) % mod;
		}
	}
	cout << ans << ‘\n‘;
} 

signed main() {
	IOS
	cin >> n >> mod;
	pre_do();
	solve();	
	return 0;
}

Codeforces Global Round 14 E

原文：https://www.cnblogs.com/mfsyflt/p/14793398.html