a?b (标量乘法)和(标量与向量乘法)经常可以省略乘号。向量点乘不能省略点乘号。
向量点乘就是对应分量乘积的和,其结果是一个标量。
a·b=|a| |b| cos ?
点乘等于向量大小约向量夹角的cos值的积。
-------------------------------------------------向量点乘(计算)----------------------------------------------
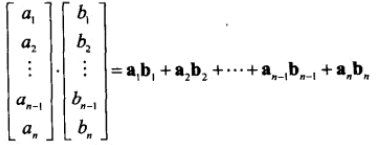

二维向量 a · b = ax bx + ay by [4,6] · [-3,7] =(4)(-3)+(6)(7)=30
三维向量 a · b = ax bx + ay by + az bz [3,-2,7] · [0,4,1]=(3)(0)+(-2)(4)+(7)(-1) =-15
点乘 = 向量大小 与 向量夹角的cos值的积;
这个是三角函数推导过来的: 推导过程 https://blog.csdn.net/dcrmg/article/details/52416832
余弦定理 https://baike.so.com/doc/5377655-5613792.html
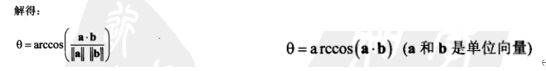
-----向量点乘(内积)(意义)----
点乘结果的符号 角度 a和b
>0 0<?<90 方向基本相同
0 ?<=90 正交
<0 90<?<=180 方向基本相反
-------------------------------------------------向量叉乘(计算)----------------------------------------------
叉乘 不满足 交换定律;
当出现叉乘和点乘时,优先计算叉乘;因为点乘返回 标量;

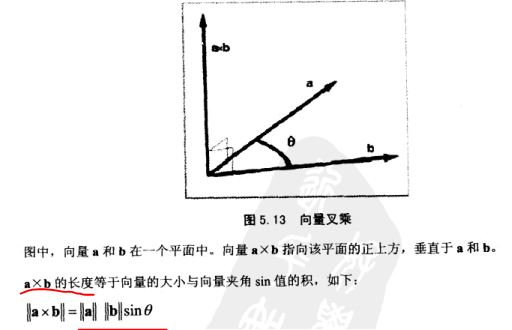
-----向量叉乘(外积)(意义)----
两个向量叉乘得到垂直于原本两个向量的向量;
-------------------------------------------------向量投影(计算)----------------------------------------------
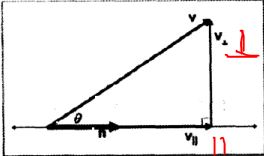
给定向量V m ,把V 分解成 V⊥ V|| ;分别垂直于平行于m;并满足V = V⊥+V||;一般称V||为V在m上的投影;
原文:https://www.cnblogs.com/yang9981/p/14788304.html