
将元素L(i)插入已有序子序列L[1,,i-1]步骤:
代码
#include<iostream>
using namespace std;
const int maxn = 20;
int a[maxn];
//带哨兵的直接插入排序
//引入哨兵可以避免很多不必要的判断语句,从而提高程序的效率
void sort1(int a[],int n)
{
for(int i=2;i<=n;i++)//依次将a[2]~a[n]插入前面已排好序的序列
{
if(a[i]<a[i-1])
{
a[0]=a[i]; //哨兵:省去了j>=0的数组越界判断
// 寻找要插入的位置
// int j=i-1;
// while(a[j]>a[0])
// {
// a[j+1]=a[j];//向后挪位
// j--;
// }
//结束while/for循环之后状态就是 a[j]<=a[0] 正好把当前的a[i]插入当前j的后面
for(j=i-1;a[j]>a[0];j--)
{
a[j+1]=a[j];
}
a[j+1]=a[0];
}
}
}
//不带哨兵的直接插入排序
void sort2(int a[],int n)
{
for(int i=2;i<=n;i++)
{
if(a[i]<a[i-1])
{
int t = a[i];
int j=i-1;
while(a[j]>t&&j) //j防止数组越界
{
a[j+1]=a[j];
j--;
}
a[j+1]=t;
}
}
}
void Print(int a[],int n)
{
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
}
int main()
{
int n; cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort1(a,n);
Print(a,n);
return 0;
}
// cout<<sizeof a/sizeof(int)<<endl; //80 20
//C++没有直接获取数组大小的变量 不同于Java Java有 数组名.length
图示
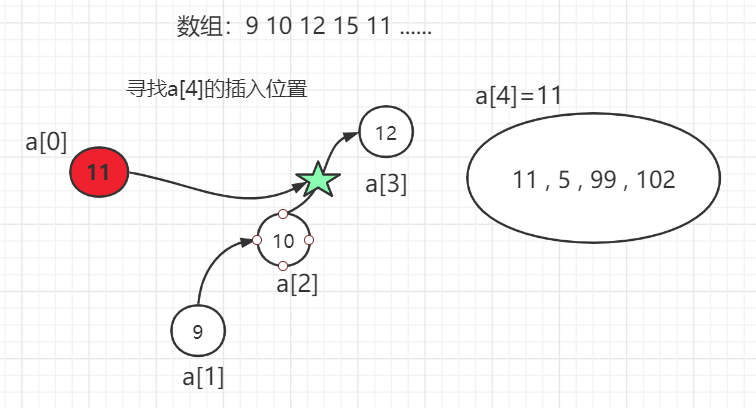
空间复杂度:O(1)
时间复杂度:n-1 趟插入元素操作,每趟操作分为比较关键字和移动元素,而比较次数和移动次数取决于待排序表的初始状态。
最好情况:数组有序,每次插入一个元素都只需要比较一次而不用移动元素。O(n)
最坏情况:数组逆序有序。比较次数最大:Σi (2<=i<=n);总的移动次数最大:Σ(i+1) (2<=i<=n)。(我觉得是Σi (2<=i<=n),但书上是Σ(i+1) (2<=i<=n))
平均情况:总的比较次数和移动次数均约为:n^2/4。
稳定的排序方法
适用于顺序存储和链式存储
前言:希尔排序为了加快速度简单的改进了插入排序,交换不相邻的元素以对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
思想:使数组中任意间隔为h的元素都是有序的。
实现:实现希尔排序的一种方式是对于每个h,用插入排序将h个子数组独立的排序。但因为子数组是相互独立的,一个更简单的方法是在h-子数组中将每个元素交换到比它大的元素之前去。只需要在插入排序的代码中将距离由1改成h即可。这样,希尔排序的实现就转化成一个类似于插入排序但使用不同增量的过程。
希尔排序更加高效的原因是他权衡了子数组的规模和有序性。排序之初,各个子数组都很短,排序之后子数组是部分有序的,这两种情况都很适合插入排序。子数组部分有序的程度取决于递增序列的选择。
代码
void sort3(int a[],int n)
{
for(int gap=n/2;gap>=1;gap/=2) //希尔排序:任意间隔h的元素都是有序的。gap即为h
{
//对每个h数组进行插入排序
for(int i=1;i<=gap;i++) //枚举h数组的起点
{
for(int j=i+gap;j<=n;j+=gap) //对以i为起点的h数组进行排序
{
if(a[j]<a[j-gap])//如果逆序
{
//移动k寻找插入位置
int t=a[j];
int k=j-gap;
while(a[k]>t&&k)
{
a[k+gap]=a[k];
k-=gap;
}
a[k+gap]=t;
}
}
}
}
}
-------------------------将两个操作分开-----------------------------------------------------------------------
void group_sort(int a[],int i,int gap,int n)
{
for(int j=i+gap;j<=n;j+=gap) //对以i为起点的h数组进行排序
{
if(a[j]<a[j-gap])//如果逆序
{
//移动k寻找插入位置
int t=a[j];
int k=j-gap;
while(a[k]>t&&k)
{
a[k+gap]=a[k];
k-=gap;
}
a[k+gap]=t;
}
}
}
void sort4(int a[],int n)
{
for(int gap=n/2;gap>=1;gap/=2) //希尔排序:任意间隔h的元素都是有序的。gap即为h
{
//对每个h数组进行插入排序
for(int i=1;i<=gap;i++) //枚举h数组的起点
{
group_sort(a,i,gap,n);
}
}
}
图解·
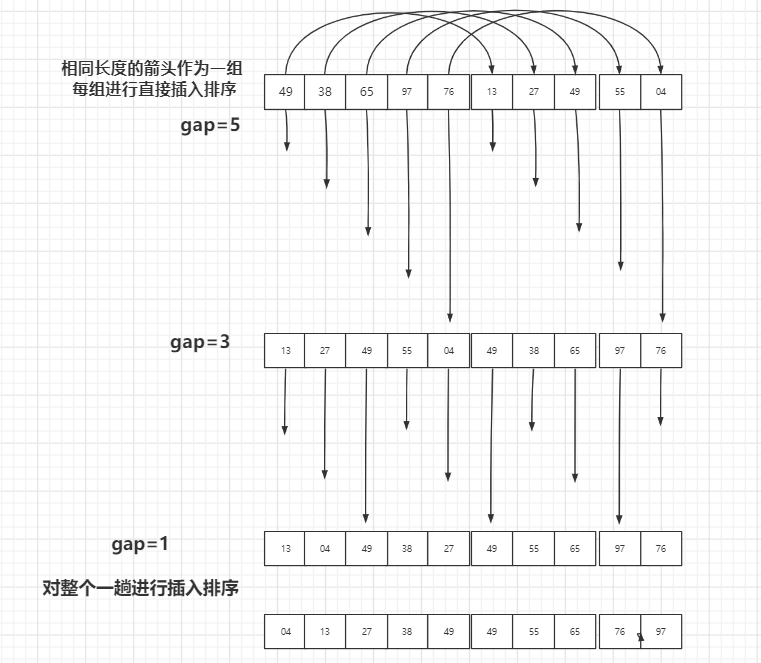
时间复杂度:O(n2)。n在某个特定范围时:O(n1.3)
空间复杂度:O(1)。
原文:https://www.cnblogs.com/4-Prestar/p/14766644.html