闫氏DP分析法——01背包为例

闫氏DP分析法

DP问题没有固定的模板，和贪心一样是一种思想。下面是DP问题的常用分析套路:

01背包

很早之前写过关于01背包的题解，但是当时的理解很杂乱。这次用Y总的方法重新理解这个问题，感觉比较清晰。
直接上代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1010;

int n,m; //n 物品数量 m 背包容量 
int v[N],w[N]; //v 体积 w 价值 
int f[N][N]; //f 状态 

int main(){
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	
	//f[0][0-m] = 0; 全局变量默认初始化
	for (int i = 1; i <= n; i ++ )
		for (int j = 0; j <= m; j ++ )
		{
		 	f[i][j] = f[i-1][j]; //  不含i 
		 	if (j >= v[i]) //背包容量j可以放下v[i] 
	 		f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
		}
			
	cout << f[n][m] << endl;
	
    return 0;
}

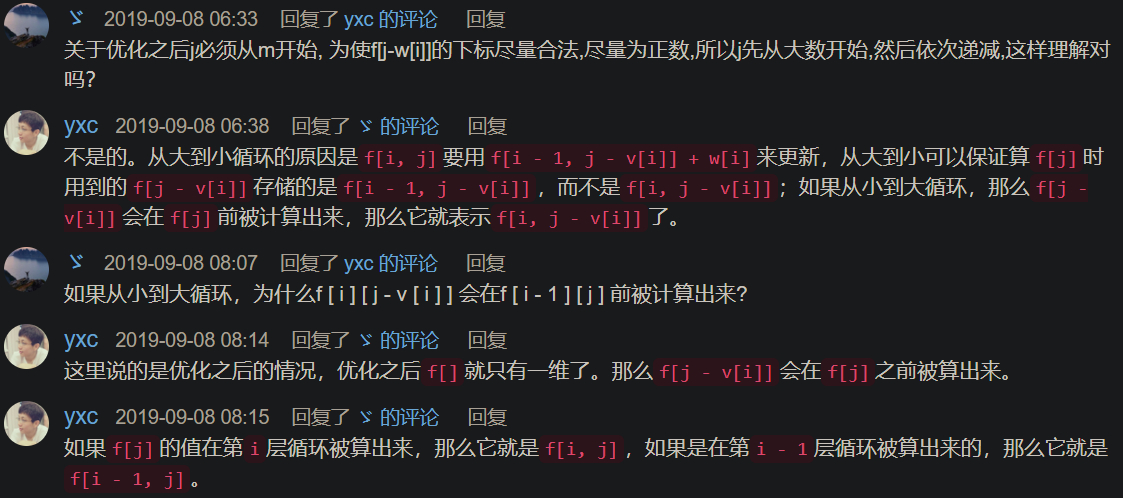
上述代码还可以优化，利用滚动数组优化成一维。
在求f[i]层只用到了f[i-1]层，并且它们的j值为j、j-v[i]都小于等于j。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1010;

int n,m; //n 物品数量 m 背包容量 
int v[N],w[N]; //v 体积 w 价值 
int f[N]; //f 状态 

int main(){
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	
	for (int i = 1; i <= n; i ++ )
		for (int j = m; j >= v[i]; j -- )
		{
		 	//f[j] = f[j]
		 	//if (j >= v[i]) //背包容量j可以放下v[i] 
	 		f[j] = max(f[j],f[j - v[i]] + w[i]);
		}
			
	cout << f[m] << endl;
	
    return 0;
}

闫氏DP分析法——01背包为例

原文：https://www.cnblogs.com/lijiaji/p/14764593.html