以经典的旅行商问题(traveling salesman problem, TSP)为例,其目标是计算出由n个给定的城市构成的一个序列,使得按此序列对这些城市的环游成本(比如机票价格)最低。尽管此类问题的描述并不复杂,但遗憾的是,由于涉及元素(比如城市)的每一排列都是一个候选解,它们往往构成一个极大的搜索空间。通常,其搜索空间的规模与全排列总数大体相当,为n! = O(n^n)。因此若采用蛮力策略,逐一生成可能的候选解并检查其是否合理,则必然无法将运行时间控制在多项式的范围以内。
为此,必须基于对应用问题的深刻理解,利用问题本身的某些规律,尽可能多 、尽可能早地排除搜索空间内的候选解。其中一种重要的技巧就是,利用候选解的某些局部特征,以候选解子集为单位批量地排除。通常如下图所示,搜索空间呈树状结构,而被排除的候选解往往属于同一分支,故这一技巧也可以形象地称作剪枝(pruning)。
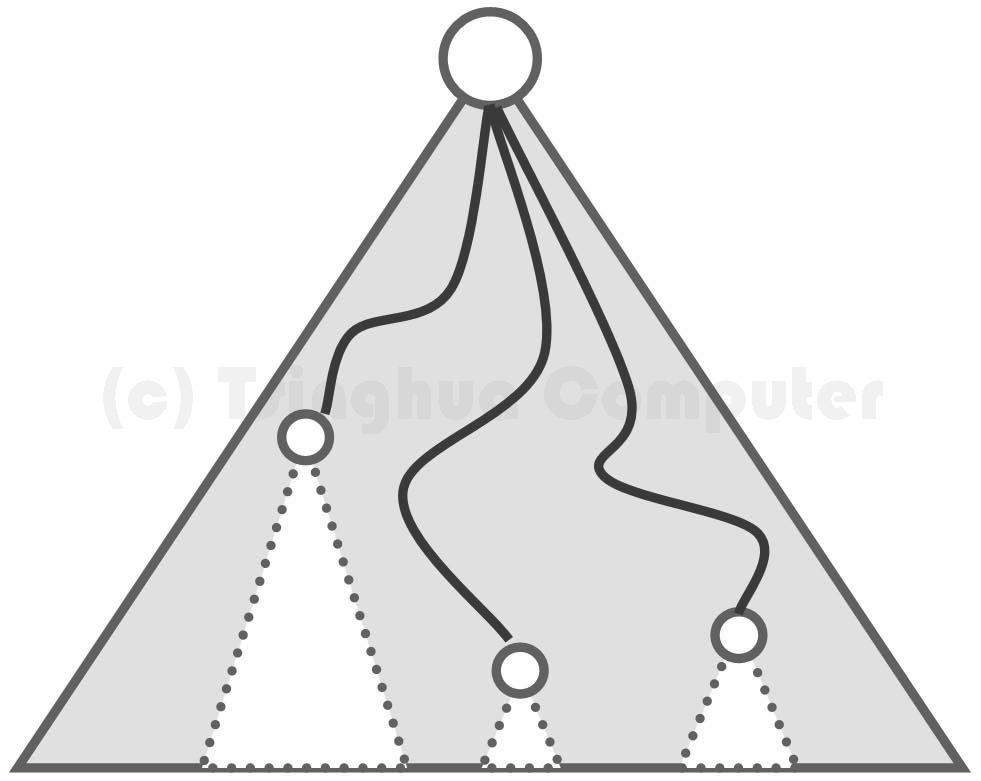
与之对应的算法多呈现如下模式。从零开始逐步增加候选解的长度。更准确地,这一过程是在成批地考察具有特定前缀的所有候选解。这种从长度上逐步向目标靠近的尝试,称作试探(probing)。作为解的局部特征,特征前缀在试探的过程中一旦发现与目标解不合,则收缩到此前一步的长度,然后继续试探下一可能的组合。特征前缀长度缩减的这类操作称作回溯(backtracking),其效果等同于剪枝。如此,只要目标解存在就迟早会被发现,而且只要剪枝所依据的特征设计得当,计算的效率就会大大提高。
N皇后问题是试探回溯策略的典型应用。基于试探回溯策略的算法可以描述如下:在第一个位置放置一个皇后,然后从下一行开始,寻找不与已有皇后冲突的位置,如果该位置的确存在,则在该位置放置一个皇后,进而转向下一行,再执行同样的过程。而一旦某一行不存在合适的位置(即该行的每一位置都与已有皇后冲突),则进行回溯,移除在上一行摆放的皇后,再从该皇后的下一位置开始试探寻找下一个合适的位置。
算法实现如下:(此处借助于向量结构实现,也可使用其他数据结构比如栈来实现)
1 struct Queen 2 { 3 int x, y; //皇后在棋盘上的坐标 4 Queen(int xx = 0, int yy = 0) : x(xx), y(yy){} 5 bool operator == (const Queen& q)const //判断两个皇后是否冲突 6 { 7 return (y == q.y) || 8 (x + y == q.x + q.y) || 9 (x - y == q.x - q.y); 10 } 11 bool operator != (const Queen& q)const 12 { 13 return !(*this == q); 14 } 15 }; 16 17 void placeQueens(Vector<Queen>& v, int N) 18 { 19 if(N < 4) 20 { 21 cout << "number " << N << " is too small!\n"; 22 return ; 23 } 24 int curx = 0, cury = 0; //当前行列 25 do 26 { 27 bool backTrack = false; //回溯标记 28 for(int y = cury; y < N; ++y) 29 { 30 backTrack = false; 31 Queen q(curx, y); 32 int size = v.size(); 33 for(int i = 0; i < size; ++i) //检查是否与已有皇后冲突 34 { 35 if(q == v[i]) 36 { 37 backTrack = true; //一旦与一个已有皇后冲突则需要回溯 38 break; 39 } 40 } 41 if(!backTrack) //与所有已有皇后都不冲突 42 { 43 v.insert(q); 44 curx++; //前进一行 45 cury = 0; //下次循环从行首开始 46 break; 47 } 48 else 49 continue; 50 } 51 if(backTrack) //如果该行没有满足条件的位置则确实需要回溯 52 { 53 curx--; //回溯一行 54 cury = v[curx].y + 1; //下次循环从上一层的下一位置开始 55 while(cury >= N) //如果需要连续回溯 56 { 57 curx--; 58 cury = v[curx].y + 1; 59 v.remove(); 60 } 61 v.remove(); 62 } 63 }while(curx != N); //N个皇后后结束循环 64 }
placeQueens将最终得到的一种可能的解存放至向量 v 中,通过遍历向量v,即可得到该解。实现如下:
1 void PrintQueen(const Vector<Queen>& v) 2 { 3 int size = v.size(); 4 for(int i = 0; i < size; ++i) 5 { 6 int cury = v[i].y; 7 for(int j = 0; j < size; ++ j) 8 { 9 if(cury == j)cout << "X "; 10 else cout<< "O "; 11 } 12 cout << endl; 13 } 14 }
测试:
1 int main() 2 { 3 Vector<Queen>v; 4 int N = 0; 5 cout << "enter a number:"; 6 cin >> N; 7 placeQueens(v, N); 8 PrintQueen(v); 9 }
结果:
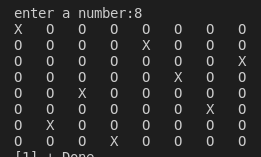
如以上结果所示,该算法确实找出了N皇后问题的一个可能解。
迷宫寻径问题是试探回溯策略的另一典型应用:在一个迷宫矩阵中,给定入口点和出口点,找到一条从入口到出口的路线(如果的确存在一条可行的路径)。
具体实现思路:设定一个前进方向的优先级,比如右(right)、下(down)、左(left)、上(up),从入口点开始,依据优先级进行试探,如果该方向可行,则继续试探,不行则依据优先级试探下一方向,如果某一位置的所有前进方向都注定会失败,则把该位置标记并回溯,根据优先级从从上一位置的下一前进方向继续试探,如此往复,只要通路的确存在,则必然可以找到一条可行的路径。
以下是迷宫寻径算法的实现:
1 struct node //坐标节点 2 { 3 int x, y; 4 node(int i1 = 0,int i2 = 0):x(i1),y(i2){} 5 void up() { --x; } //向某一方向前进一个单位 6 void down() { ++x; } 7 void left() { --y; } 8 void right() { ++y; } 9 bool operator==(const node&n) 10 { 11 return x == n.x && y == n.y; 12 } 13 bool operator!=(const node& n) 14 { 15 return !(*this == n); 16 } 17 }; 18 19 20 enum class Direction //方向 21 { 22 Right, Down, Left, Up, Unknown 23 }; 24 25 26 bool is_path(const node& n, Direction d, int** maze, int rows, int cols) //判断坐标某一方向是否可行 27 { 28 switch (d) //不能越界 不能是尝试过的失败坐标 29 { //也不能是标记为已访问的坐标 30 case Direction::Right: 31 return n.y + 1 < cols && maze[n.x][n.y + 1] != 1 && 32 maze[n.x][n.y + 1] != 4 && maze[n.x][n.y + 1] != 6; 33 case Direction::Down: 34 return n.x + 1 < rows && maze[n.x + 1][n.y] != 1 && 35 maze[n.x + 1][n.y] != 4 && maze[n.x + 1][n.y] != 6; 36 case Direction::Left: 37 return n.y - 1 >= 0 && maze[n.x][n.y - 1] != 1 && 38 maze[n.x][n.y - 1] != 4 && maze[n.x][n.y - 1] != 6; 39 case Direction::Up: 40 return n.x - 1 >= 0 && maze[n.x - 1][n.y] != 1 && 41 maze[n.x - 1][n.y] != 4 && maze[n.x - 1][n.y] != 6; 42 } 43 return false; 44 } 45 // 迷宫地图 起点 终点 路线 46 void find_path(int** maze, int rows, int cols, node beg, node end, Vector<node>& path) 47 { 48 node cur = beg; 49 maze[cur.x][cur.y] = 6; //将走过的坐标标记为6 50 Direction d = Direction::Unknown; //用来记录上一步的方向 51 path.insert(cur); 52 while (cur != end && maze[beg.x][beg.y] != 4) //每次要排除前一步的方向 53 { 54 if (is_path(cur, Direction::Right, maze, rows, cols) && d != Direction::Left) 55 { 56 cur.right(); 57 maze[cur.x][cur.y] = 6; 58 path.insert(cur); //可行就将该坐标放入容器保存 59 d = Direction::Right; 60 } 61 else if (is_path(cur, Direction::Down, maze, rows, cols) && d != Direction::Up) 62 { 63 cur.down(); 64 maze[cur.x][cur.y] = 6; 65 path.insert(cur); 66 d = Direction::Down; 67 } 68 else if (is_path(cur, Direction::Left, maze, rows, cols) && d != Direction::Right) 69 { 70 cur.left(); 71 maze[cur.x][cur.y] = 6; 72 path.insert(cur); 73 d = Direction::Left; 74 } 75 else if (is_path(cur, Direction::Up, maze, rows, cols) && d != Direction::Down) 76 { 77 cur.up(); 78 maze[cur.x][cur.y] = 6; 79 path.insert(cur); 80 d = Direction::Up; 81 } 82 else //如果四个方向都不行就回溯 83 { 84 maze[cur.x][cur.y] = 4; //将尝试失败的坐标标记为4 85 path.remove(); 86 cur = path[path.size() - 1]; //回溯一次 87 switch (d) //回溯的方向也要记录 88 { 89 case Direction::Right: 90 d = Direction::Left; 91 break; 92 case Direction::Down: 93 d = Direction::Up; 94 break; 95 case Direction::Left: 96 d = Direction::Right; 97 break; 98 case Direction::Up: 99 d = Direction::Down; 100 break; 101 } 102 } 103 } 104 if (maze[beg.x][beg.y] == 4)cout << "no path to destination!\n"; 105 else 106 cout<<"find path to destination!\n"; 107 }
通过find_path即可找到迷宫maze中从出口到入口的一条通路,并保存该路径上的所有坐标节点到向量path中。
测试:(迷宫中1为障碍物)
1 static int cells[20][20] = //迷宫地图 2 { 3 0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1, 4 1,0,0,1,0,1,0,0,0,1,1,0,0,1,1,1,0,0,0,0, 5 1,1,0,0,0,1,1,1,1,0,1,1,0,0,1,0,1,0,1,1, 6 1,1,1,1,0,1,1,0,0,0,0,1,1,0,1,0,0,0,0,1, 7 0,0,0,0,0,1,0,0,1,0,0,1,1,0,1,1,0,1,0,1, 8 0,1,0,1,0,1,1,0,1,0,1,0,1,0,1,0,0,1,0,0, 9 1,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0, 10 1,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,0,1, 11 1,0,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1, 12 1,1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,1,1,0,0, 13 0,1,1,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,1, 14 0,1,1,0,0,1,1,0,1,0,1,0,1,0,1,0,1,0,0,1, 15 0,0,1,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,1,1, 16 1,0,0,0,1,0,1,0,1,0,1,0,1,0,0,0,0,0,1,1, 17 1,1,1,0,1,0,0,0,1,1,0,0,1,1,1,0,1,1,1,1, 18 1,0,0,0,0,1,1,0,0,1,1,1,1,0,0,0,1,0,0,1, 19 1,1,1,1,0,1,1,1,0,0,0,0,0,1,1,1,0,1,0,1, 20 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,1, 21 1,1,1,0,1,0,1,1,0,0,0,0,0,0,0,0,1,1,1,1, 22 1,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,0,0 23 }; 24 25 26 int main() 27 { 28 int rows = 20; 29 int cols = 20; 30 int** maze = new int* [rows]; 31 for (int i = 0; i < rows; ++i) 32 maze[i] = cells[i]; 33 34 node beg(0, 0); //起点 35 node end(19, 19); //终点 36 Vector<node>path; //保存坐标用的向量 37 find_path(maze, rows, cols, beg, end, path); 38 if (path.size())cout << path.size() << " steps takes" << endl; 39 for (int i = 0; i < 20; ++i) 40 { 41 for (int j = 0; j < 20; ++j) 42 { 43 cout << maze[i][j]; 44 } 45 cout << endl; 46 } 47 delete[]maze; 48 }
结果:
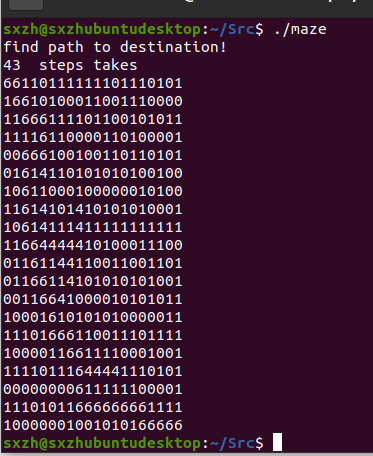
如图,的确在起点(0, 0),终点(19, 19),之间找到了一条通路(由上图中数字6组成),此外,find_path 也确实将试探失败的坐标标记为了4。
原文:https://www.cnblogs.com/sxzh/p/14752900.html