难度 medium
在一棵无限的二叉树上,每个节点都有两个子节点,树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示,在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。
给你树上某一个节点的标号 label,请你返回从根节点到该标号为 label 节点的路径,该路径是由途经的节点标号所组成的。
示例 1:
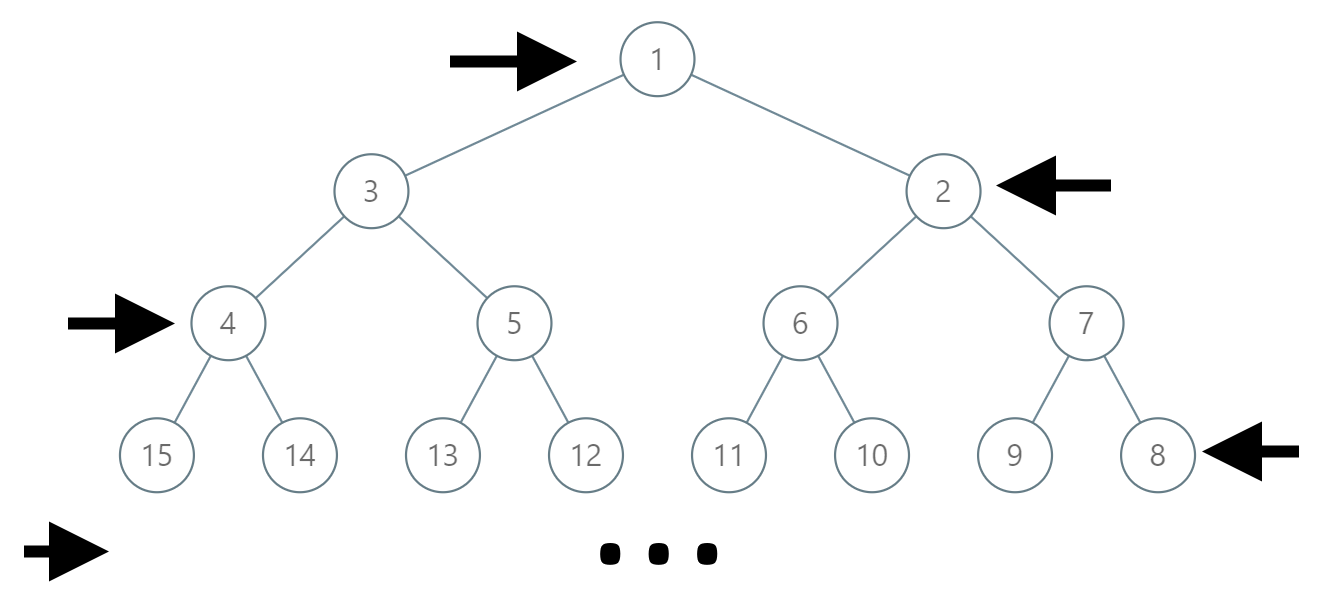
输入:label = 14
输出:[1,3,4,14]
示例 2:
输入:label = 26
输出:[1,2,6,10,26]
提示:
1 <= label <= 10^6
解题思路:这道题目其实没有什么难度,主要就是坐标的关系分析起来比较麻烦,想不到一种简洁优雅的做法,说一下我怎么想的,首先还是找到log2(label),其实就是确定树的深度,记为n,然后用一个数组res记录结果,先把label加进去,然后求这个label在上一层属于哪个节点,这里用label%pow(2, i),i是从n-1到0递减的一个数,就是表示当前在哪一层,用一个变量t = (int) (label % Math.pow(2, i))表示从按递增的顺序来数当前这个数前面有几个数,这里就是 14%pow(2,3)=6,然后用一个变量pos = (int) Math.ceil((double)(t+1) / 2),表示在上一层按数字递减的顺序,当前节点的父节点应该排在第几位,除以2是因为上一层的节点数比这一层少一个,这里就是第4位,因为上一层是按递减的顺序来,所以没有必要分奇偶,这里最简单的就是用起点Math.pow(2, i-1)加长度Math.pow(2, i-1)减去递减的pos位,于是得到新的label,继续网上遍历即可。
代码 t39 s71 java
class Solution {
public List<Integer> pathInZigZagTree(int label) {
int n = 0;
while (Math.pow(2, n)<=label) n++;
List<Integer> res = new ArrayList<>();
res.add(label);
for(int i=n-1; i>0; i--){
int t = (int) (label % Math.pow(2, i));
int pos = (int) Math.ceil((double)(t+1) / 2);
label = (int)(Math.pow(2, i-1)*2 - pos);
res.add(label);
}
Collections.reverse(res);
return res;
}
}
解题思路2:这里leecode的题解提供了一种更加清晰严谨的解法,其实思路和我这种差不多,但是把过程都推算得非常详细了,我重新思考了一下,其实解决过程可以更加简化,只要找到规律即可,以14为例,如果我们的二叉树是那种正常从左到右递增的二叉树,上一层的节点应该为14/2=7,但是这里变成了4,主要就是上一层的节点都倒置了,4和7对称,5和6对称,因此我们还是可以用label/2,先找到它原本应该对应的节点,然后再找对称点就可以了,这个对称点在哪里呢?leetcode我参考的那个题解用了很长很长的公式推导,最后得到的结果就是,以第m层为例,label = 3 * Math.pow(2, m) - label/2 - 1,其实可以这样理解,Math.pow(2, m)就是上一层的最小节点,而最大节点应该怎么求呢?每一层的最后一个节点就是2*Math.pow(2, m)-1,因为这一层的最小的节点就是Math.pow(2, m+1),上一层的最大节点肯定比当前层最小节点小一,因此我们把上一层最大和最小节点加起来,就是相互对称的两个数的和,减去label/2,就是label对应的父节点对应的值。代码如下。
代码 t38 s53 java
class Solution {
public List<Integer> pathInZigZagTree(int label) {
int n = (int)(Math.log(label) / Math.log(2));
List<Integer> res = new ArrayList<>();
res.add(label);
while(n>0){
label = (int)(3 * Math.pow(2, --n) - 1 - (label/2));
res.add(label);
}
Collections.reverse(res);
return res;
}
}
原文:https://www.cnblogs.com/zhengxch/p/14742537.html