1、大O表示法

大O表示法并不是具体代码执行的时间，而是标识代码执行时间随数据规模增长的变化趋势。当数据规模很大的时候，只需要记录最大量级就可以了。比如实际复杂度为:

最终用大O表示法为：

因为当n非常大的时候2n和3的大小是可以忽略的

2、时间复杂度分析

2.1 只关注执行次数最多的一段代码

示例代码：

public int sum(int n)
{
    int sum=0;
    for(i=0; i< j; i++)
    {
    	 sum=sum + i;
    }
    return sum;
}

以上代码只需要关注那个for循环即可(执行n次)，其他赋值等操作为常数级复杂度，与n的数量级没有关系，所以上面代码的复杂度为：O(n)

2.2 加法法则，总复杂度等于量级最大的代码的复杂度

示例代码：

public int sum(int n)
{
    int sum=0;
    for(i=0; i< n; i++)
    {
    	 sum=sum + i;
    }
    
    int sum2=0;
    for(i=0; i< n; i++)
    {
    	 for(j=0;j<n;j++)
    	 {
    	 	  sum = sum + i *j
    	 }
    }
    return sum + sum2; 
}

以上复杂度为O(n) + O(n^{2)，基于上面的分析，取最大量级，得知最终的复杂度为O(n}2)。

2.3 乘法法则，嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

示例代码：

public int calculate(int n)
{
    int sum=0;
    for(i=0; i< n; i++)
    {
    	 sum=sum + fun(i);
    }
}

public int fun(int n)
{
    int sum=0;
    for(i=0; i< n; i++)
    {
    	 sum=sum + i;
    }
    return sum;
}

以上复杂度为O(n) * O(n)，为O(n^2)。

3、常见时间复杂度示例

3.1 O(1)

O(1)表示常数级执行次数，并不是表示只执行一次。

public int calculate()
{
    int i=1;
    int j=2;
    return i+j
}

以上代码执行了3次，是个常数级别，其复杂度是O(1)，而不是O(3)。

3.2 O(logn)

代码：

public void fun(int n)
{
    int i=0;
    while(i < n)
    {
        i= i*2;
    }
}

上述循环的执行次数所多少呢。

k即为循环的执行次数：

所以复杂度为O(logn)。

4、复杂度量级

4.1 多现实量级

1. 常亮阶O(1)
2. 对数阶O(logn)
3. 线性阶O(n)
4. 线性对数阶O(nlogn)
5. 平方阶O(n^{2）。。。k次方阶O(n}k）

4.2 非多项式量级（NP)

1. 指数阶O(2^n)
2. 阶乘阶O(n!)

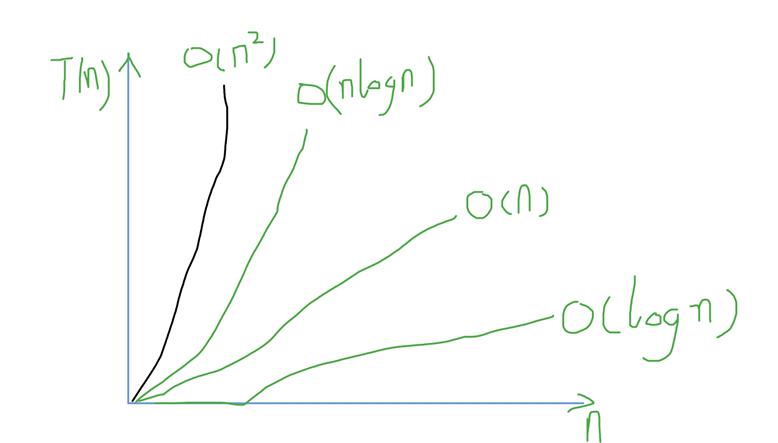
当N越来越大时，非多项式级算法的执行时间会急剧增加，效率非常低下。

算法复杂度分析

原文：https://www.cnblogs.com/Brake/p/14729568.html