几何 手拉手模型及夹半角模型

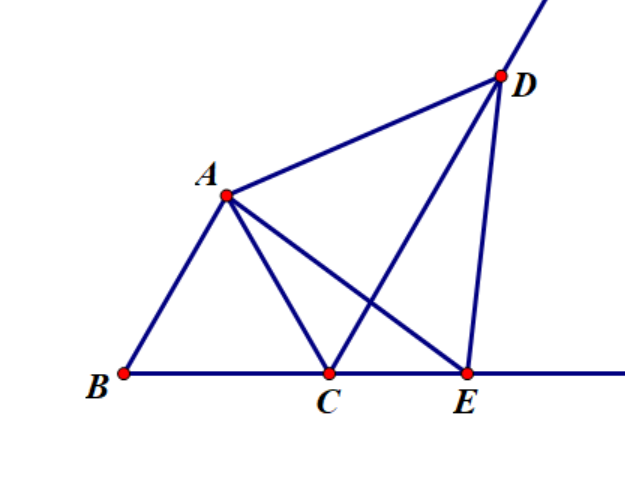
Q: 如图,有两个等边 $\triangle ABC,\triangle ADE$ 且 $B,C,E$ 三点共线,求证 $CD$ 平分 $\angle ACE$

A:

$\because AB=AC,AE=AD,\angle BAE=\angle CAD$

$\therefore \triangle ABE\cong \triangle ACD$

$\therefore \angle ACD=\angle ABC=60^{\circ}$

$\because \angle ACE=120^{\circ}$

$\therefore CD$ 平分 $\angle ACE$

像这样两个相似三角形(题中等边三角形)共顶点,连接剩下两顶点来构造全等三角形的模型叫作手拉手模型

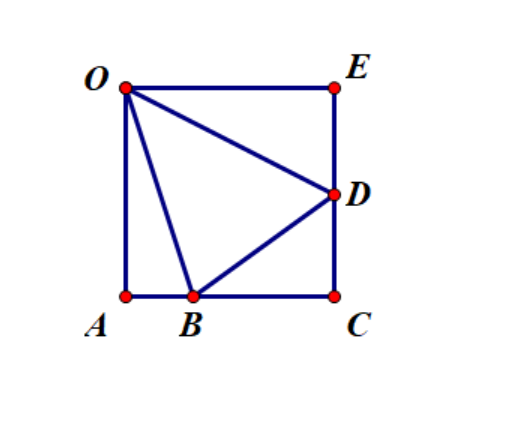
Q: 如图$,\square OACE$ 内 $\angle BOD=45^{\circ},$求证 $AB+DE=BD$

A: 如图$,OE=EG,OF=OB$

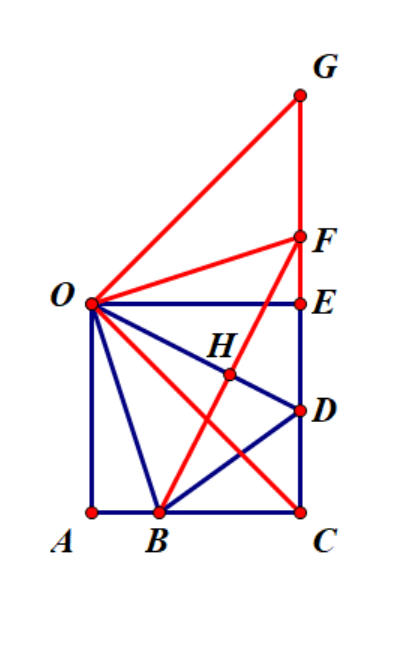
显然$,\because \triangle OAB\cong \triangle OEF,\triangle OAC\cong \triangle OEG$

$\therefore \triangle OBC\cong \triangle OFG$

$\therefore \angle BOF=\angle COG=90^{\circ}$

$\because \angle BOD=45^{\circ}$

$\therefore OD$ 是等腰直角 $\triangle OBF$ 一边 $BF$ 的垂直平分线

$\therefore \triangle DBF$ 等腰

$\therefore BD=DF=DE+EF=DE+AB$

这就是夹半角模型

几何 手拉手模型及夹半角模型

原文：https://www.cnblogs.com/zhangshaojia/p/14729742.html