(1)树的顺序存储结构:对于一颗树所有节点按照层序自顶向下,同一层自左向右。
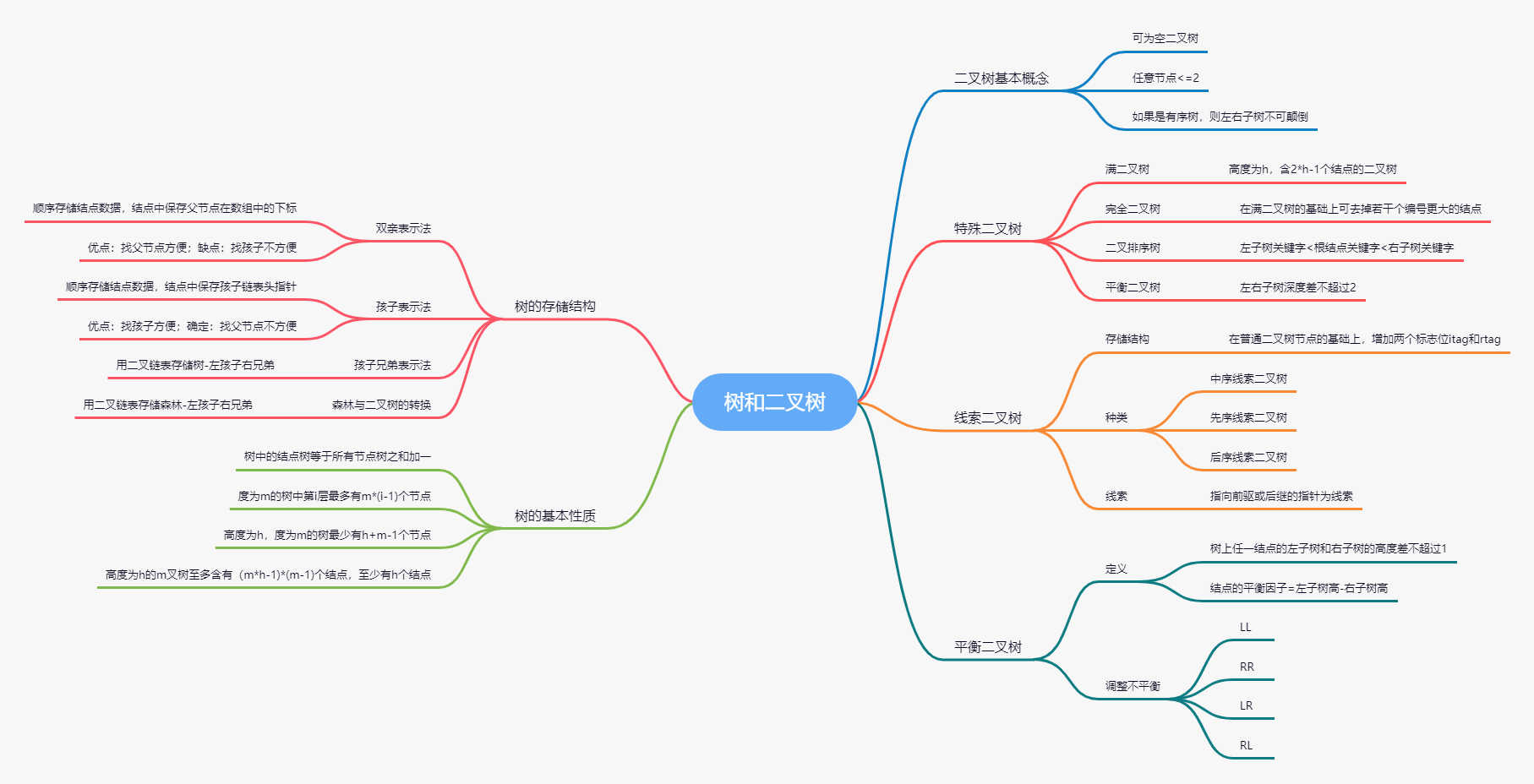
(2)二叉树是一个有限的结点集合,这个集合或者为空,或者由一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成
void PreOrder(BTNode* b) { //先序遍历递归算法 if (b != NULL) { printf("%c", b->data); //访问根节点 PreOrder(b->Ichild); //先序遍历左子树 PreOrder(b->rchild); //先序遍历右子树 } } void InOrder(BTNode* b) { //中序遍历递归算法 if (b != NULL) { InOrder(b->Ichild); //中序遍历左子树 printf("%c", b->data); //访问根节点 InOrder(b->rchild); //中序遍历右子树 } } void PostOrder(BTNode* b) { //后序遍历递归算法 if (b != NULL) { PostOrder(b->Ichild); //后序遍历左子树 PostOrder(b->rchild); //后序遍历右子树 printf("%c", b->data); //访问根节点 } }
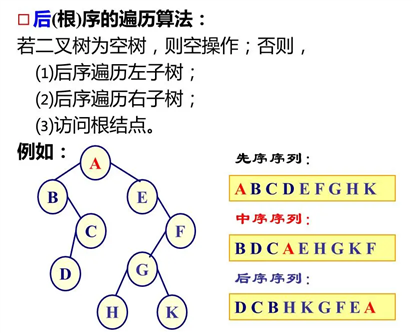
BTNode* CreatBT(char* pre, char* in, int n) { //pre存放先序序列,in存放中序序列,n为二叉树结点个数 BTNode* b; char* p; int k; if (n <= 0)return NULL; b = new BTNode; //创建二叉树结点b b->data = *pre; for (p = in; p < in + n; p++) { //在中序遍历中找等于*pre字符的位置 if (*p == *pre)break; //pre指向根节点 } k = p - in; //确定根节点在in中的位置 b->Ichild = CreatBT(pre + 1, in, k);//递归构造左子树 b->rchild = CreatBT(pre + 1 + k, in, k);//递归构造右子树 return b; }
定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树。
路径:在一棵树中,一个结点到另一个结点之间的通路。
路径长度:在一条路径中,每经过一个结点,路径长度加1。
结点的权:给每一个结点赋予一个新的数值。
结点的带权路径长度:指的是从根节点到该结点之间路径长度与该结点的权的乘积。
原文:https://www.cnblogs.com/BrBr/p/14723319.html