树与二叉树

1.思维导图

2.重要概念

哈夫曼树的原理与构造

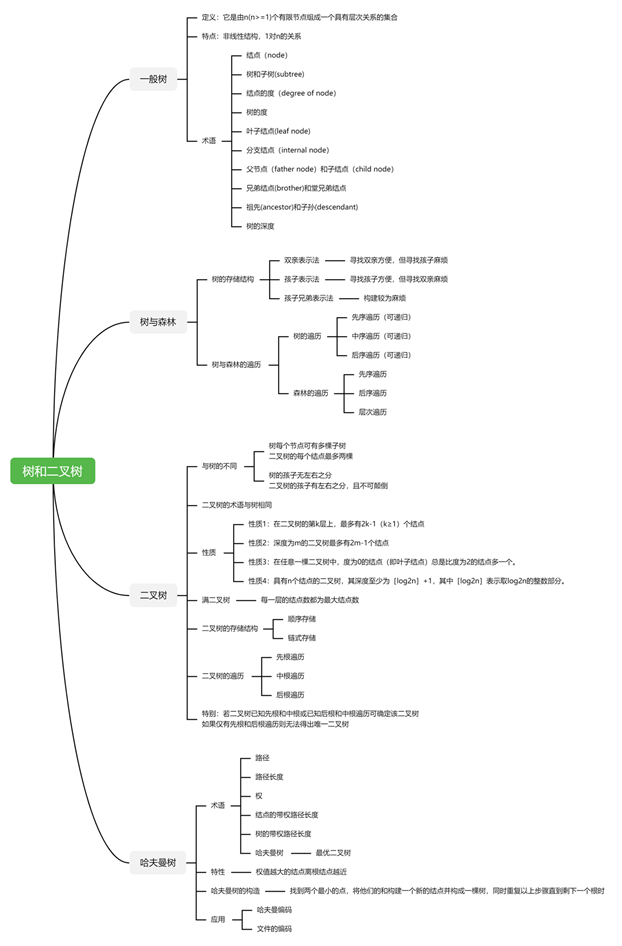
1.哈夫曼树的概念：给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)

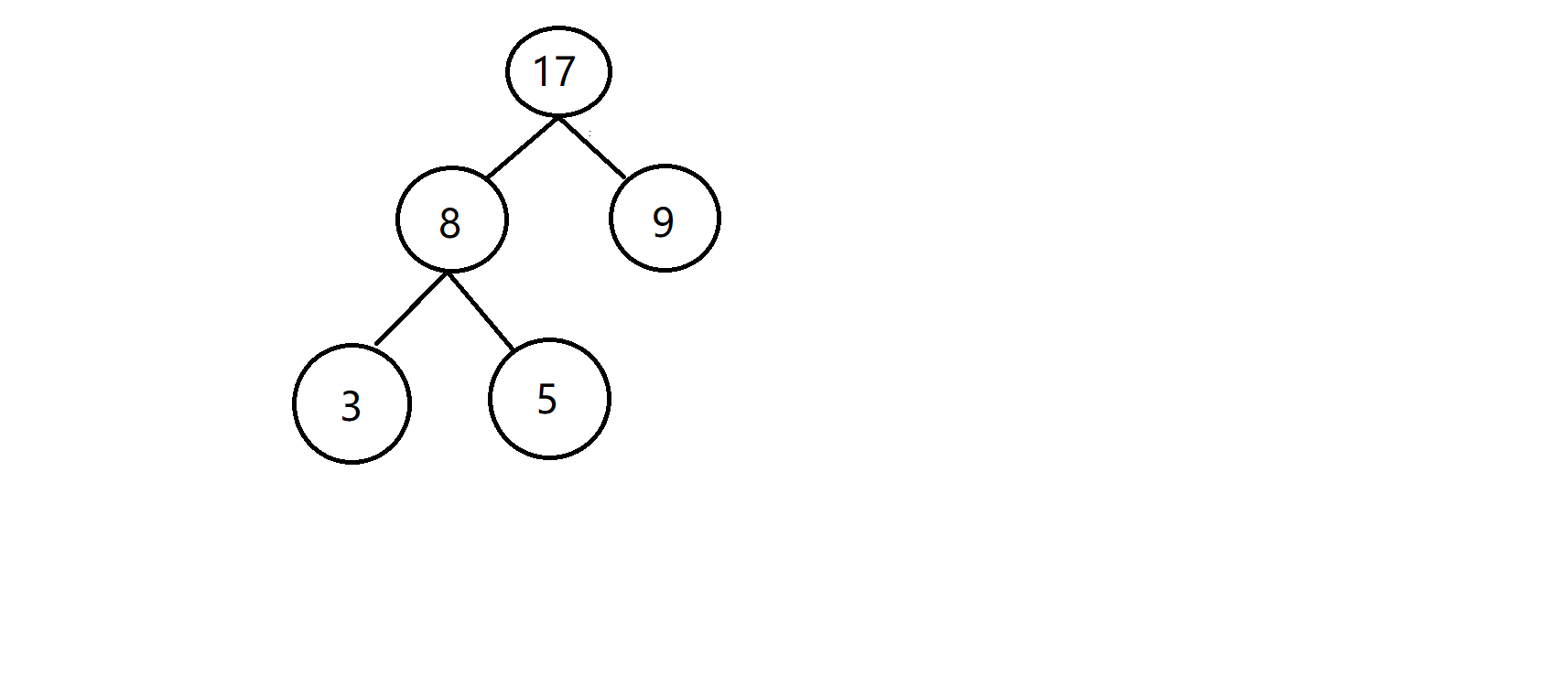
如图即为一个简单的哈夫曼树，该树的带权路径长度 （3 * 2+5 * 2+9 * 1）=25

2.哈夫曼树的构造：

给定N个权值分别为w1, w2, ..., Wn的节点。构造哈夫曼树的算法描述如下：
1）将这N个结点分别作为N棵树仅含一个结点的二叉树，构成森林F.
2）构造一个新节点，并从F中选取两棵根结点权值最小的树作为新节点的左、右子树，并且将新节点的权值置为左、右子树上根结点的权
值之和。
3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
4）重复步骤2和3，直至F中只剩下一棵树为止。

（可能看定义十分麻烦，所以干脆举个例子）

比如给一组数字{2，123，23，43，5，55，71，65}

（1）首先先找到数组中两个最小的数字，2与3，将他们的和作为结点，2，3分别作为左右子树，构造一棵新树，并且删除2，3结点，将5放入数组中，则数组为{7，123，23，43，55，71，65}

（2）重复步骤一直到数组中仅有一个数字，即仅有一个根、

这就是哈夫曼树的构成

3.哈夫曼树的代码实现

利用数组方式构建（数组大小有哈夫曼树中结点个数决定，若结点个树为N，则根据哈夫曼树的构造可知，至少要生成N-1个新节点，则数组大小为2N-1）

1.首先构建哈夫曼树中的结点

struct Htnode{
	int weight,parent,lchild,rchild;
	char c; 
};
//每个哈夫曼树有结点，双亲，左孩子，右孩子

2.构造哈夫曼树

void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n)
{ 
    /* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，
        x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
    int i, j, m1, m2, x1, x2;
    /* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
    for (i=0; i<2*n-1; i++)
    {
        HuffNode[i].weight = 0;//权值 
        HuffNode[i].parent =-1;
        HuffNode[i].lchild =-1;
        HuffNode[i].rchild =-1;
    } 
    /* 输入 n 个叶子结点的权值 */
    for (i=0; i<n; i++)
    {
        printf ("Please input weight of leaf node %d: \n", i);
        scanf ("%d", &HuffNode[i].weight);
    } /* end for */
 
    /* 循环构造 Huffman 树 */
    for (i=0; i<n-1; i++)
    {
        m1=m2=MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
        x1=x2=0;
        /* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */
        for (j=0; j<n+i; j++)
        {
            if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
            {
                m2=m1; 
                x2=x1; 
                m1=HuffNode[j].weight;
                x1=j;
            }
            else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
            {
                m2=HuffNode[j].weight;
                x2=j;
            }
        } 
            /* 设置找到的两个子结点 x1、x2 的父结点信息 */
        HuffNode[x1].parent  = n+i;
        HuffNode[x2].parent  = n+i;
        HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
        HuffNode[n+i].lchild = x1;
        HuffNode[n+i].rchild = x2;
        }

树与二叉树

原文：https://www.cnblogs.com/sleep-early/p/14721146.html