1、定义

二叉搜索树（Binary Search Tree），（又：二叉查询树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

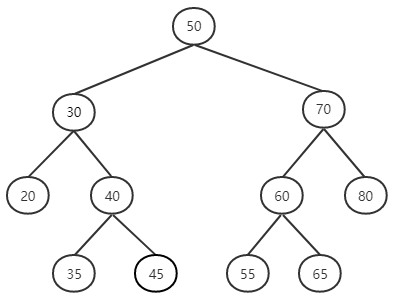
通俗地讲，以当前节点为根，其左右子树的特点：左小右大。当前节点为50时，其左子树所有节点均小于50，右子树所有节点均大于50：

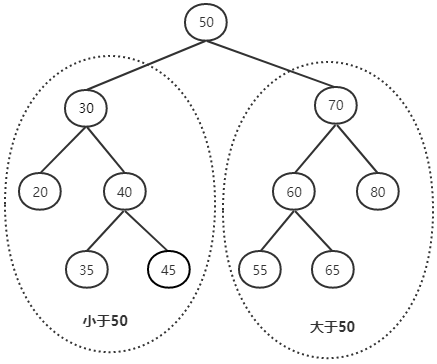
节点50的左右子树也同样符合这种特点，以左子树为例（以30为根的树）：

2、查找

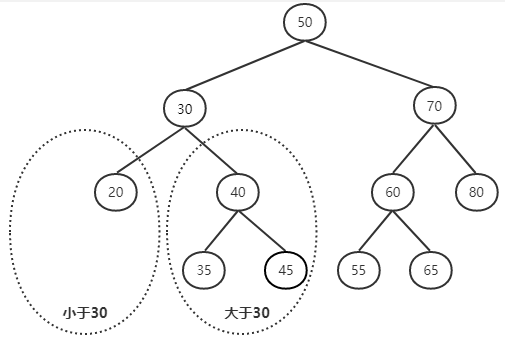
根据左小右大的特点，查找一个元素时，从根节点出发：

• 如果查找的元素比当前节点小，则到左子树找；
• 如果查找的元素比当前节点大，则到右子树找；
• 如果查找的元素等于当前节点，说明找到了；
• 如果直至叶子节点都找不到对应的，说明该元素不存在该树中。

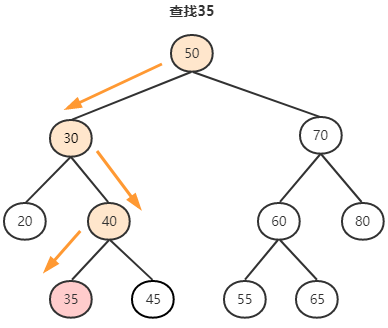
流程图如下：

3、插入

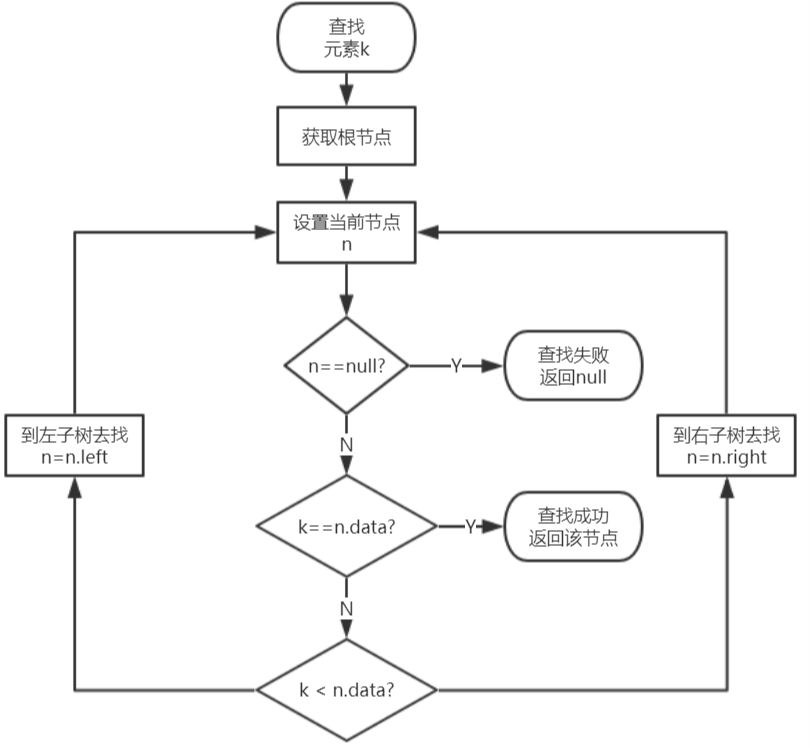
流程图

4、删除

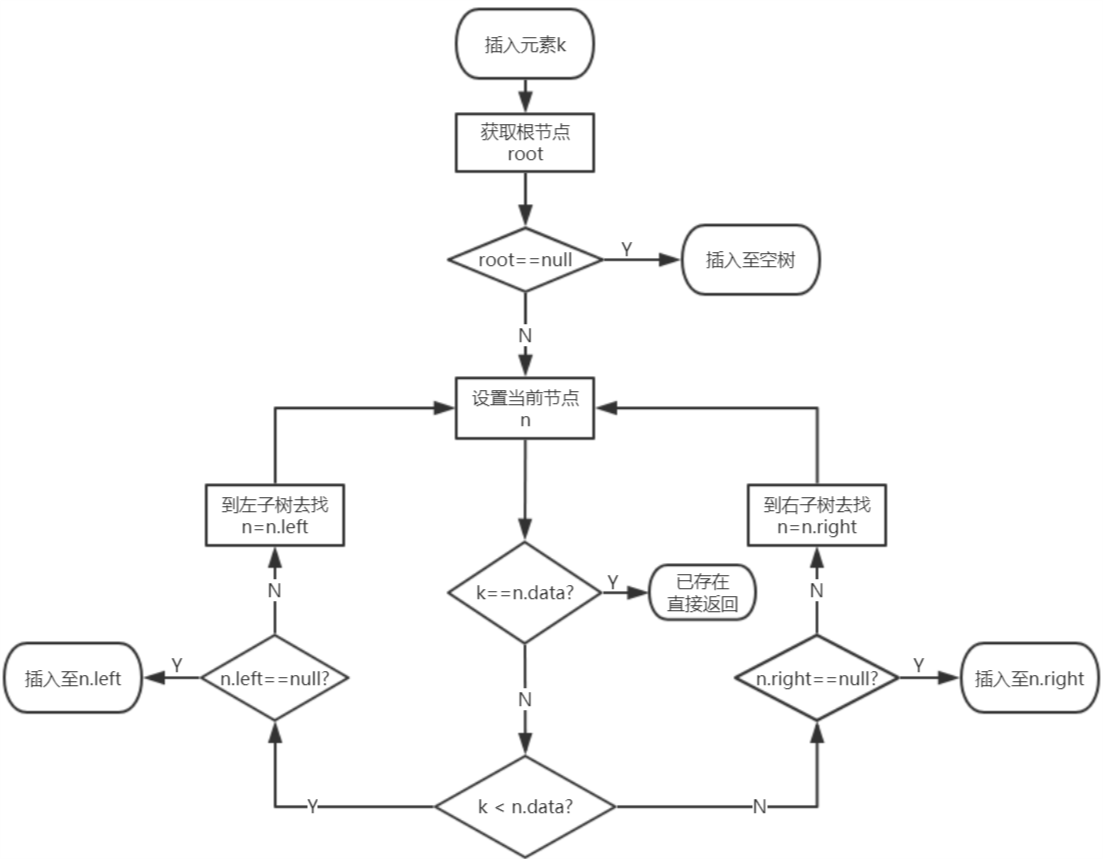
删除前首先要找到该节点，如果找不到，直接结束即可。找到后，可以分为以下三种情景：

• 无子节点，即叶子节点，直接删除即可；
• 只有一个子节点，用该子节点接到删除节点的父节点即可；
• 有两个子节点，使用前或后继节点作为替换节点，对删除节点进行数据替换，然后转移至删除替换节点即可。而此时删除后继节点时，必然是情景1或2了；

5、二叉搜索树的问题

极端时，搜索的时间复杂度将会降低到 O(n)，比如以下这个例子：

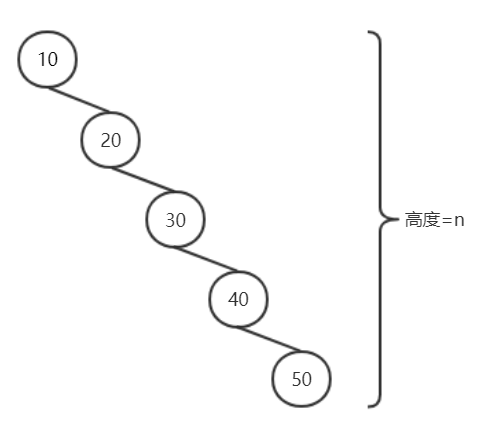
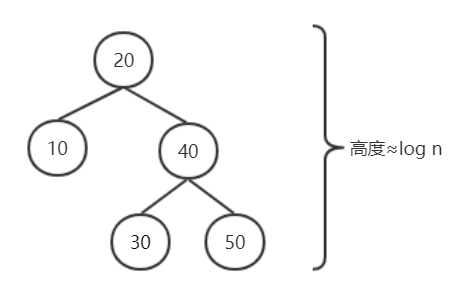
而平衡二叉搜索树（AVL树、红黑树等）就是为了解决这个问题：平衡二叉树在进行插入、删除后，会进行自平衡，从而保证其查询的时间复杂度接近于O(log2n)。如红黑树连续插入10,20,30,40,50：

Binary Search Tree

原文：https://www.cnblogs.com/zhongqifeng/p/14684784.html