杨辉三角小性质

求杨辉三角中数\(n(1\le n\le1e9)\)最先出现的位置

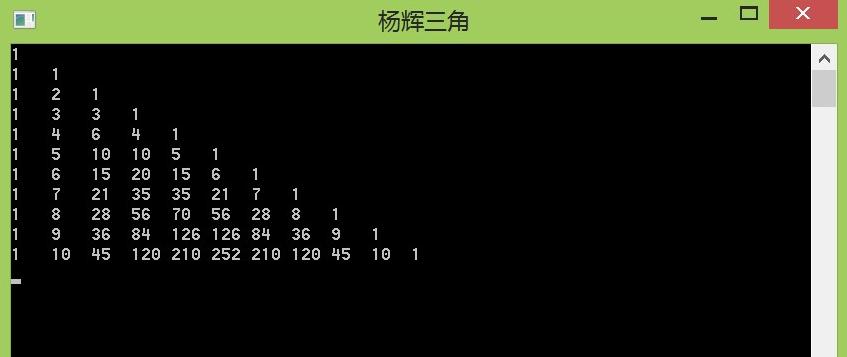
\(dp[i][j]=dp[i][j-1]+dp[i-1][j-1]+....dp[1][j-1]\)

那么对于每一列单独考虑

第一列为\(1\;1\;1\;1...\)

第二列为\(1\;2\;3\;4...\)

第三列为\(1\;3\;6\;10...\)

每一列的第\(i\)个元素都是上一列前\(i\)个元素的前缀和

除去一二列

那么第三列的元素到达\(10^9\)这个数量级差不多\(1e5\)个数 递增为\(n^2\)

第四列元素递增为\(n^4\)

第五列为\(n^8\)

递增为指数型上涨，那么利用前缀和，对于每一列求出值为\(n\)的位置(可能没有)

然后取最优解即可

杨辉三角小性质

原文：https://www.cnblogs.com/hunxuewangzi/p/14673559.html