理论：参考链接
Beta分布是二项式分布的共轭先验分布，而狄利克雷(Dirichlet)分布是多项式分布的共轭分布。
共轭的意思是，以Beta分布和二项式分布为例，数据符合二项分布的时候，参数的先验分布和后验分布都能保持Beta分布的形式，这种形式不变的好处是，我们能够在先验分布中赋予参数很明确的物理意义，这个物理意义可以延续到后续分布中进行解释，同时从先验变换到后验过程中从数据中补充的知识也容易有物理解释。
计算过程：参考链接
文档-主题矩阵：
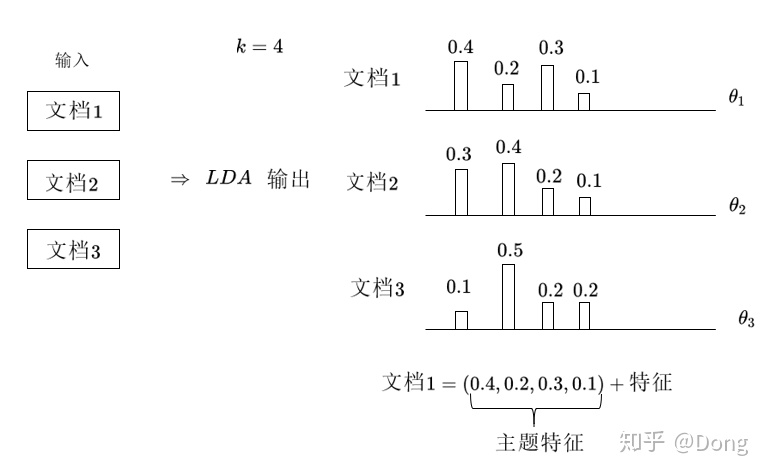
主题-单词矩阵：
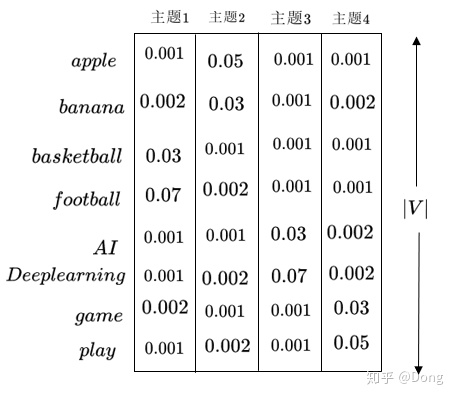
参数说明：
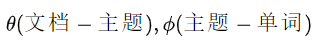
训练方法：
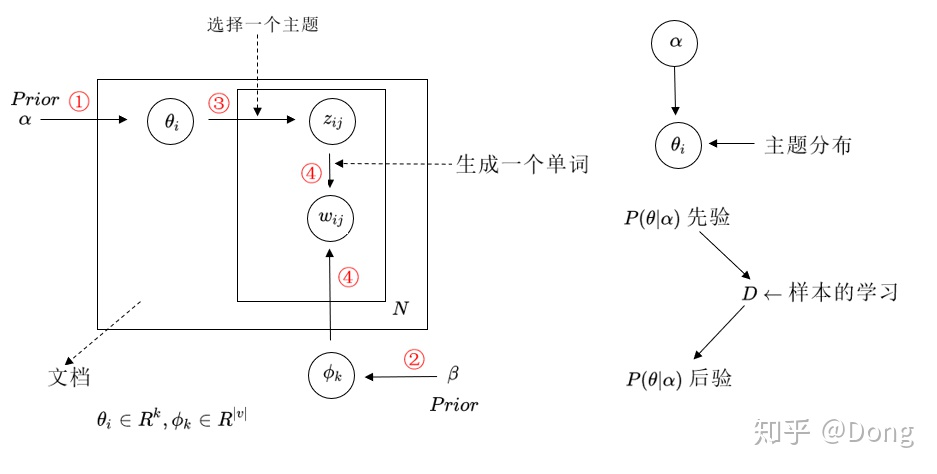
通过样本的学习不断调整先验概率,最后学出一个参数的分布
z为主题词，w为单词。所以：
（1）两个先验分布分别生成主题词的分布和单词的分布
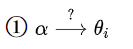
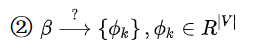其中|V|是单词的个数，所以相当于单词的概率，K是主题的个数，对每个主题，它对每个单词都有概率。
（2）由主题词分布生成主题词，再由主题词生成单词
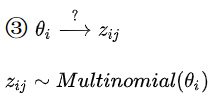
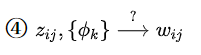
整个LDA训练的流程：
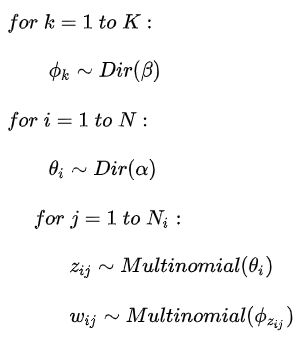
通过样本的学习不断调整先验概率,最后学出一个参数的分布。
原文：https://www.cnblogs.com/Joyce-good-girl/p/14668325.html