Prim算法
什么是最小生成树?
例子:镇长管辖6个村落,分别是A村、B村、C村、D村、E村、F村。镇长住A村,他想去其他各个村落视察,但没有路过不去,所以要修路。但是两两村落间修路所需的钱不同,如下图所示:A村到B村需6万元,B村到C村需3万元……。村长是个小气鬼,想花最少的钱确保他能到每一个村落视察。
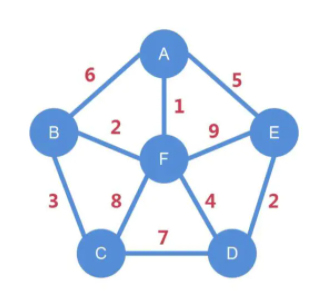
那么如何修路呢?
下面介绍用Prim算法修路,即寻找最小生成树
镇长到A村,先选择A村相邻花费最少的(1万)到F村,再选择F村相邻花费最少的(2万)到B村,再选择B村相邻花费最少的(3万)到C村,接下来C村只能选择到D村,但花费太多了(7明显在上图中不是个小数目),镇长不同意,故保留。接着往回退到F村,F村到D村(4万),D村到E村(2万)。即下图
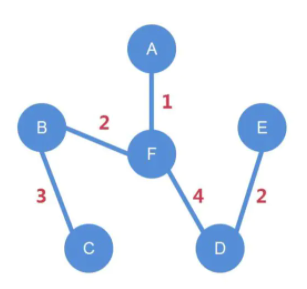
这样,镇长就能花最少的钱,愉快的到每个属于他的村落装13了。
PS:镇长不关心其余村落间方不方便,是不是花最少的钱。只关心他住的地方(A村)是不是花最少的钱能到每个村落。
上图就是一个最小生成树,即花最少的钱修连接所有村落的路。
最小生成树:边的权重之和最小的那棵生成树。
什么是生成树?
生成树是图的极小连通子图。极小连通子图,即任意掐断一条路,就会存在结点与其他结点断开;任意添加一条路,就会形成回路。
故最小生成树首先是生成树,其次是边的权重之和最小。
Kruskal算法
将森林构成一棵树。选权重最小的连接,如果构成了回路则放弃,继续找权重小的连接,直至成为一棵树。
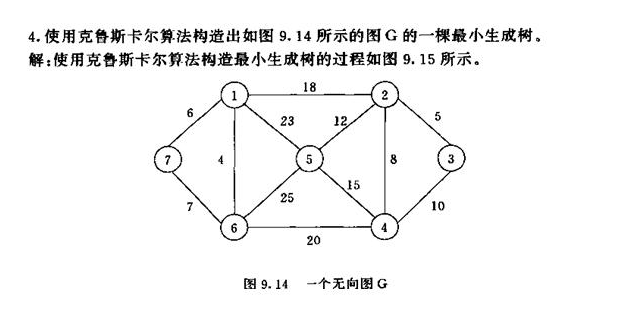
先将权重最小的(权重是4)连接,再将权重5连接,权重6连接,此时不能连接权重7的,因为权重4,权重6已经连接,此时连接权重7则会形成回路,故放弃,再去将权重8的连接,权重10不能连接,权重5,权重8,权重10会形成回路。权重12连接,权重15不能连接,因为权重8,12,15会形成回路。权重18连接。
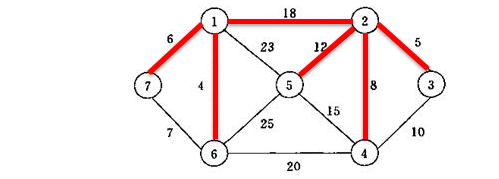
此时结点1可到达所有的结点。最小生成树已经形成。
原文:https://www.cnblogs.com/jinlin-2018/p/14659659.html