Monte-Carlo Tree Search

Motivation

We all know that Monte Carlo Simulation is used to estimate some unknown variables through random simulation. It is because that the process is too complicated so we cannot know the true rule behind it. Only god knows. But thankful to the randomness we can do lots of experiments to approach the truth.

MCTS has the same idea but it is based on a tree. Every path from root to leaf forms a solution and the whole tree defines the search space. It is a heuristic search strategy based on some loss functions. But it will follow not only the loss but also try to explore the unvisited nodes. So it‘s also trying to make a balance between exploration & exploitation.

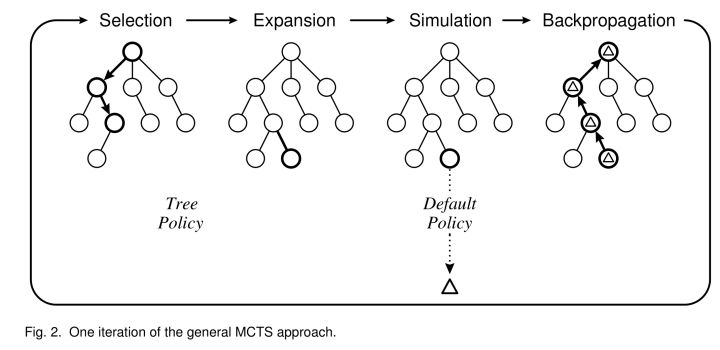
One iteration has 4 processes: Selection, Expansion, Simulation and Backpropagation. Let‘s start to build the tree.
Initially the tree only has a root node. Every node holds 3 info: action list for the next decision; visit times to measure the exploration; quality values to measure the exploitation.

1. Selection
   Using some criterion to select a child node which is eager to expand. There are 3 possibilities for the current state:
   If all the actions have been expanded thus the node has finished a complete search, then we will find a child with max UCB value and go down the tree recursively;
   Else if there are still some actions which have not been expanded (e.g. the node has 20 possible actions but there are 19 child node in the tree), then it will select one action randomly from the unexpanded actions and do Step 2 Expansion;
   Else game over and do Step 4 Backpropagation.
2. Expansion
   We have found the most eager node N to expand and the action A after Selection. So we need to add a new node S to the tree as N‘s child node by doing A.
3. Simulation/Playout
   Start from S to let the game run randomly until game over. Then we get a performance to be S‘s initial quality value.
4. Backpropagation
   The nodes along the path from root to N will update their quality values after S‘s simulation.

After some fixed number of iterations or time limit, we will get a large tree and select the best leaf node as the result. Below is a figure:

Upper Confidence Bound (UCB)

When we need to select a child node to go down the tree, we usually use UCB criterion:

\(\hat\mu_{child}\) is the average reward gathered over all tree-walks with prefix child, \(n(s)\) the number of the parent‘s visits and \(C\) is constant controlling exploration & exploitation. UCB tends to select a node with high quality value (for exploitation) and relatively low visit times (for exploration).

An example

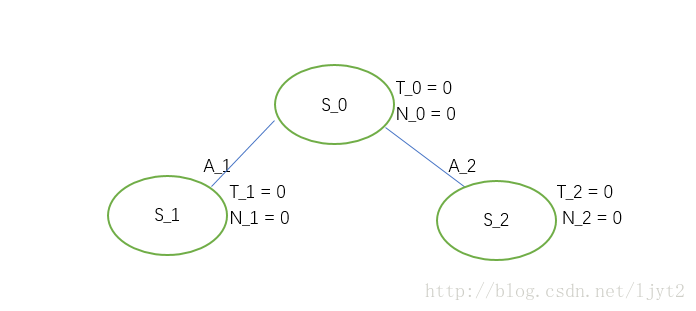
1. Initial tree
   Actually we only have root node \(S_0\). Assume there are only two actions.
   
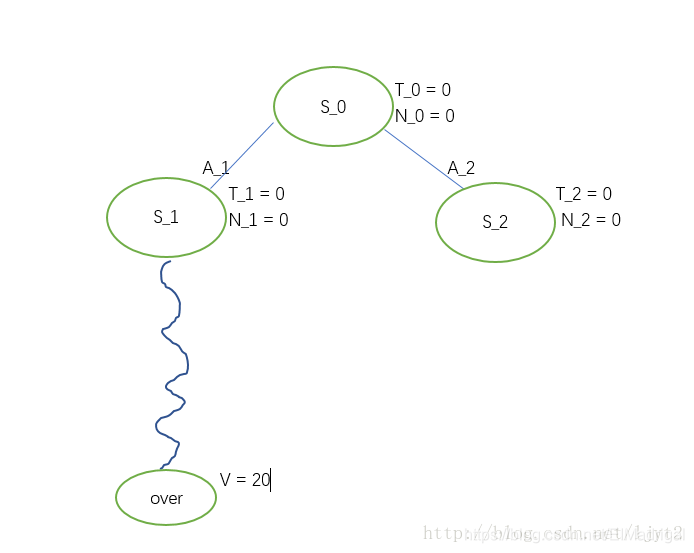
2. First Iteration
   Since the 2 actions are both unexpanded so we randomly select one (assume we select \(A_1\)). Then we add \(S_1\) to the tree and playout from \(S_1\).
   
   We got a performance of 20 and then backpropagate to \(S_1\) and \(S_0\). We finished the first iteration.
   
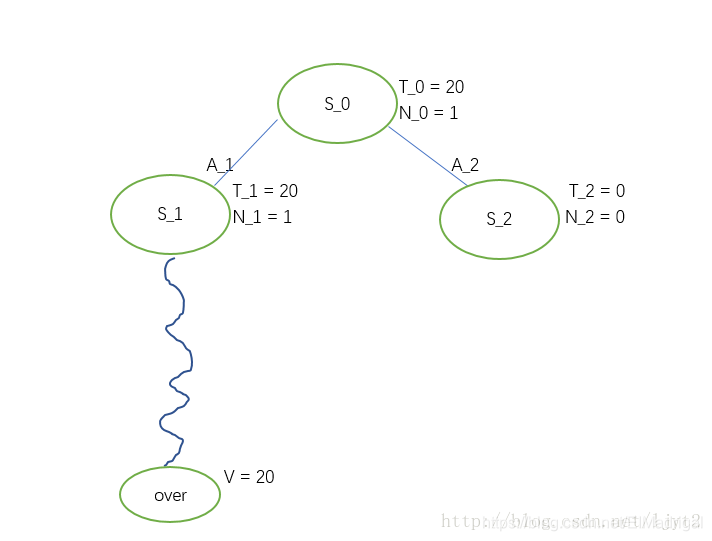
3. Second iteration
   Start from \(S_0\), since \(A_2\) has not been expanded so we have to choose it. Then add \(S_2\) to the tree and playout from here.
   
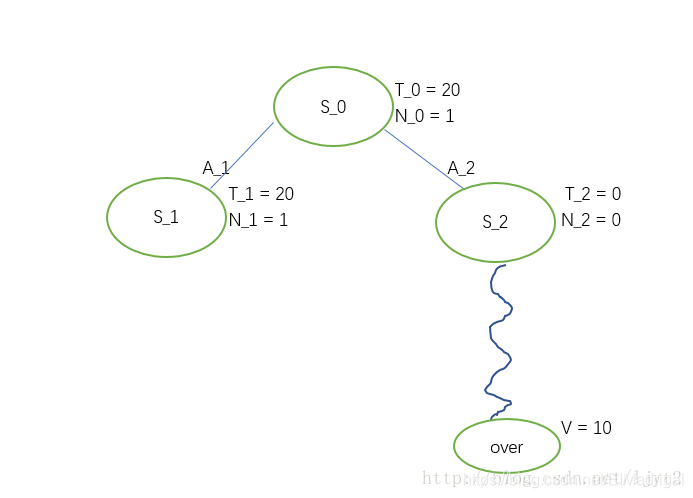
   Then backpropagate to \(S_2\) and \(S_0\):
   
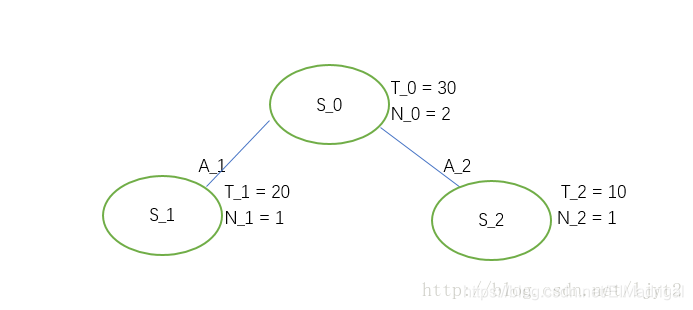
4. Third iteration
   From \(S_0\) there are no unexpanded actions so we need to select one child using UCB (assume C=2). \(UCB(S_1)=21.67,UCB(S_2)=11.67\). Thus we select \(S_1\). Assume \(S_1\) has 2 unexpanded actions:
   
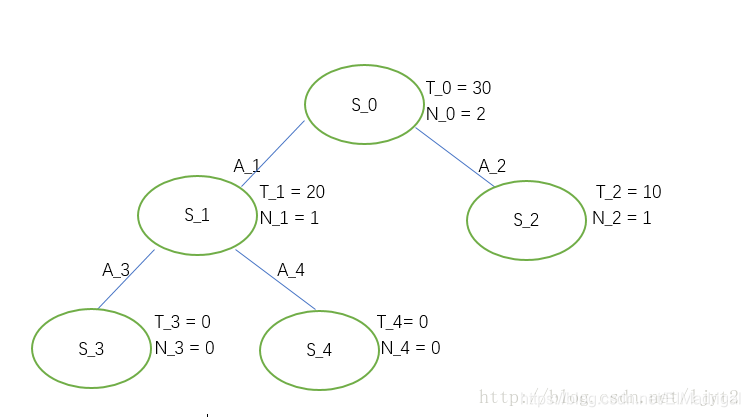
   Choose one randomly (assume \(S_3\)) and playout from here and backpropagate.

After 4 iterations we can get a tree below:

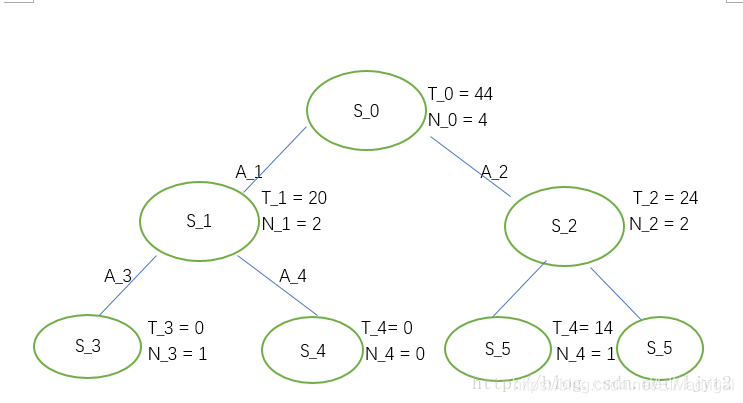
Finally we can select the best solution from \(S_0\) to leaf node.

Monte-Carlo Tree Search

原文：https://www.cnblogs.com/EIMadrigal/p/14655033.html