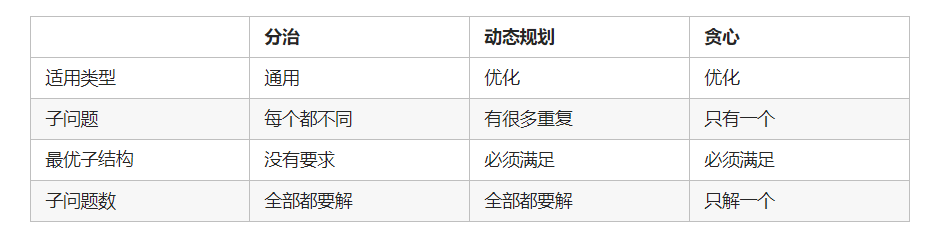
1.动态规划一般是两种形式:最优子结构和重复子问题。
对于最优子结构,一般指的是子问题与原问题的关系,通过将原问题分解为子问题,得到子问题的最优解,再将子问题最优解组合起来,得到原问题的最优解,如f(n)=f(n-1)+f(n-2).
对于重复子问题,一般指的是子问题之间的关系,在递归计算每个子问题的最优解时,如果有大量重复计算(如果没有,那就使用普通递归就可以),那么可以通过保存计算过程中的状态减少重复计算。
解决动态规划问题的核心就是处理子问题与子问题或原问题之间的关系。
2动态规划和分治、贪心的区别(简单理解)
分治是将规模减小,有时候减小一个,有时候减小一半,然后将每个小问题的解以及当前的情况组合起来得出最终的结果。如归并排序,快速排序等。与动态规划的区别是,动态规划会有重复子问题计算,而分治不会出现重复,两个区间的数据不会重叠,没有子问题重复出现。
贪心:
对于最优子结构问题:
(1)贪心:每一步的最优解一定包含上一步的最优解,上一步之前的最优解无需记录
(2)动态规划:全局最优解中一定包含某个局部最优解,但不一定包含上一步的局部最优解,因此需要记录之前的所有的局部最优解
关于子问题最优解组合成原问题最优解的组合方式:
贪心:如果把所有的子问题看成一棵树的话,贪心从根出发,每次向下遍历最优子树即可,这里的最优是贪心意义上的最优。此时不需要知道一个节点的所有子树情况,于是构不成一棵完整的树
动态规划:动态规划需要对每一个子树求最优解,直至下面的每一个叶子的值,最后得到一棵完整的树,在所有子树都得到最优解后,将他们组合成答案
结果正确性:
贪心不能保证解得的结果是最优的,复杂度低
动态规划最终的结果一定是最优解,复杂度高(因为将所有结果都计算了一遍,比较后得到的最优结果,本质是穷举法)
以上内容来自leetcode动态规划精讲
原文:https://www.cnblogs.com/xiaomaoli/p/14622083.html