目录
分治算法即分而治之,就是把一个复杂的问题分解成两个或多个相同或相似的子问题,再把子问题分解成更小的问题。。。直到最后子问题可以简单地直接求解,原问题即子问题的合并。分治算法主要分为三个步骤:
(此例子引用连接如下:https://www.zhihu.com/search?type=content&q=%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95)
有这样一个经典的问题:有100枚硬币,其中1枚重量与众不同,是假币,更轻一些。如果用天平秤,请问至少称多少次一定能找到这枚假币
加入我们用传统的枚举法,显然至少需要比较50次
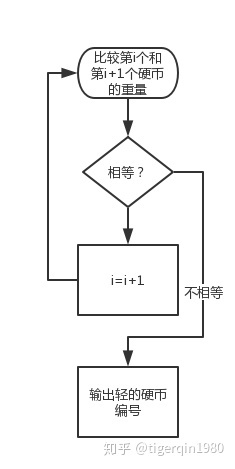
而假设我们采用分治法的话 ,流程如下:1. 将100硬币分成3份,33,33,34。
2.称量1、2份,若天平平衡,则假币必在另外34枚中。若不平衡,假币在轻的那33枚里。
3.将34枚分为11/11/12枚(或将33枚分成11*3)。
4.称量两组11枚的硬币,若平衡,假币在12枚里(或另外的11枚)若不平衡,假币在轻的11里。
5.将11(或12)枚分成3/4/4(或4/4/4),称量4/4,方法同上。
6.将剩下的3(或4)分为1/1/1(或1/1),称量1/1,若平衡,则剩下的一枚是假币,若不平衡,轻的是假币。 若还剩4枚,出现1/1平衡,剩下2枚则称量,显然轻的是假币。
这种方法只需要5次就能解决这个问题。
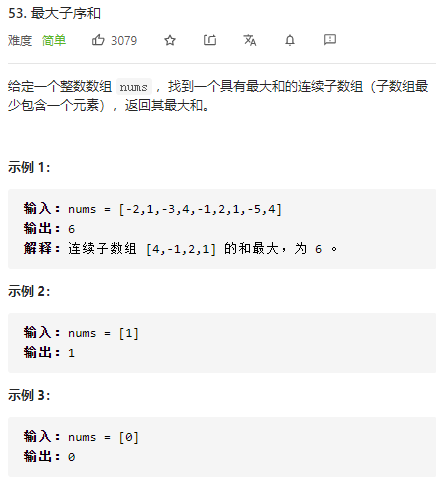
解决此问题有两种方法:
设置一个当前最大值和全局最大值,遍历整个数组,当此时的最大值小于0时,则前面的都不要,否则,将下一个数相加即可
1 class Solution { 2 public: 3 int FindGreatestSumOfSubArray(vector<int> array) { 4 /* 5 要实现求得连续子数组的最大和,我们可以 6 */ 7 if(array.empty()) 8 return 0; 9 int cursum=0; 10 int maxsum=array[0]; 11 for(int i=0;i<array.size();++i) 12 { 13 if(cursum<=0) 14 cursum=array[i]; 15 else 16 { 17 cursum+=array[i]; 18 } 19 if(cursum>=maxsum) 20 maxsum=cursum; 21 } 22 return maxsum; 23 } 24 };
要找到最大连续和的子数组,我们可以用分治算法,设最左边为left,最右边为right,中间节点为mid,则最大子数组可以分为以下三种情况:
1. 最大连续子数组都左边子数组[left, mid]
2. 最大连续子数组都在右边子数组[mid+1,right]
3. 最大连续子数组跨越了中点,一部分在左边子数组中,一部分在右边子数组中
最大连续子数组一定是三种情况中的最大值
1 class Solution { 2 /* 3 要找到连续最大子序和,我们可以用分治算法,设最左边为left, 最右边为right,中间节点为mid,则最大连续子数组可能情况为以下三种: 4 1. 最大连续子数组都在[left, mid]中 5 2. 最大连续子数组都在[mid+1, right]中 6 3. 最大连续子数组跨越了中点,因此left<=i<=mid<=j<=right 7 */ 8 //只需要在这三种情况中找出最大值即可 9 //首先是求出mid在子数组中间的情况 10 /* 11 我们的目的是找出mid在子数组中的子数组的和 12 */ 13 int INT_MIN=-2147483648; 14 public int find_max_cross_substr(int[] nums,int left,int mid,int right) 15 { 16 int maxleft=0,maxright=0; 17 int sum=0; 18 int leftsum=INT_MIN,rightsum=INT_MIN; 19 //首先找到左半边子数组的最大值 20 for(int i=mid;i>=left;--i) 21 { 22 sum+=nums[i]; 23 leftsum=Math.max(sum,leftsum); 24 } 25 //然后找到右半边子数组的最大值 26 sum=0; 27 for(int j=mid+1;j<=right;++j) 28 { 29 sum+=nums[j]; 30 rightsum=Math.max(sum,rightsum); 31 } 32 return (leftsum+rightsum); 33 } 34 //然后进行递归查找,比较三种情况,找出最大值 35 public int find_max_substr(int[]nums,int left,int right) 36 { 37 if(left==right) 38 return nums[left];//找到递归结束条件,结束递归 39 else 40 { 41 int mid=left+(right-left)/2; 42 int maxleftsum,maxrightsum,maxcrosssum; 43 maxleftsum=find_max_substr(nums,left,mid); 44 maxrightsum=find_max_substr(nums,mid+1,right); 45 maxcrosssum=find_max_cross_substr(nums,left,mid,right); 46 return Math.max(Math.max(maxleftsum,maxrightsum),maxcrosssum); 47 } 48 49 } 50 public int maxSubArray(int[] nums) { 51 return find_max_substr(nums,0,nums.length-1); 52 } 53 }
1 class Solution { 2 /* 3 要找到连续最大子序和,我们可以用分治算法,设最左边为left, 最右边为right,中间节点为mid,则最大连续子数组可能情况为以下三种: 4 1. 最大连续子数组都在[left, mid]中 5 2. 最大连续子数组都在[mid+1, right]中 6 3. 最大连续子数组跨越了中点,因此left<=i<=mid<=j<=right 7 */ 8 //只需要在这三种情况中找出最大值即可 9 //首先是求出mid在子数组中间的情况 10 /* 11 我们的目的是找出mid在子数组中的子数组的和 12 */ 13 int INT_MIN=-2147483648; 14 public int find_max_cross_substr(int[] nums,int left,int mid,int right) 15 { 16 int maxleft=0,maxright=0; 17 int sum=0; 18 int leftsum=INT_MIN,rightsum=INT_MIN; 19 //首先找到左半边子数组的最大值 20 for(int i=mid;i>=left;--i) 21 { 22 sum+=nums[i]; 23 leftsum=Math.max(sum,leftsum); 24 } 25 //然后找到右半边子数组的最大值 26 sum=0; 27 for(int j=mid+1;j<=right;++j) 28 { 29 sum+=nums[j]; 30 rightsum=Math.max(sum,rightsum); 31 } 32 return (leftsum+rightsum); 33 } 34 //然后进行递归查找,比较三种情况,找出最大值 35 public int find_max_substr(int[]nums,int left,int right) 36 { 37 if(left==right) 38 return nums[left];//找到递归结束条件,结束递归 39 else 40 { 41 int mid=left+(right-left)/2; 42 int maxleftsum,maxrightsum,maxcrosssum; 43 maxleftsum=find_max_substr(nums,left,mid); 44 maxrightsum=find_max_substr(nums,mid+1,right); 45 maxcrosssum=find_max_cross_substr(nums,left,mid,right); 46 return Math.max(Math.max(maxleftsum,maxrightsum),maxcrosssum); 47 } 48 49 } 50 public int maxSubArray(int[] nums) { 51 return find_max_substr(nums,0,nums.length-1); 52 } 53 }
原文:https://www.cnblogs.com/Cucucudeblog/p/14611867.html