上一节我们完成了渲染管线的搭建。该渲染管线是一个高度简化过的管线,只保留了传入模型网格、简单顶点着色、简单片元着色、光栅化写入双缓冲这几个步骤。由于上篇的篇幅较长,因此把光栅化的具体算法留在本篇来讲。
我们一共要完成两部分内容:分别是已知两个点,绘制其中的直线(画线操作)、已知三角形的三个点,填充三角形内部像素(填充操作)。
首先是画线操作。直线一共有4种基础状态,分别是横线、竖线和两种45°角的斜线:
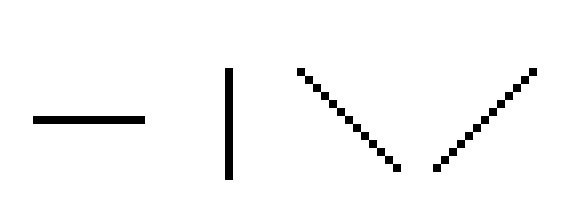
既然要画线,我们就必须要得出直线的函数表达式。斜截式(y=kx+b)是我们最熟悉的直线公式,只要我们给出一个x,就能得到相应的y值。但是在图2种,很显然给出一个x,我们得到的是无数个y,导致这个问题出现的原因是没有正确的选择自变量。
上述图中,图1必须让x作为自变量,y作为因变量;图2必须让y作为自变量,x作为因变量;图3、图4则随意。不难总结出以下判断方式:计算两点之间的横坐标差值△x和纵坐标差值△y,比较一下|△x|和|△y|之间的大小,若|△x|更大,则以x为自变量;否则以y作为自变量。
对于上述四张图而言,只要写出对应的y=kx+b或x=my+n即可精确的定位每个像素的位置,但是对于下述两张图而言会出现新的问题:
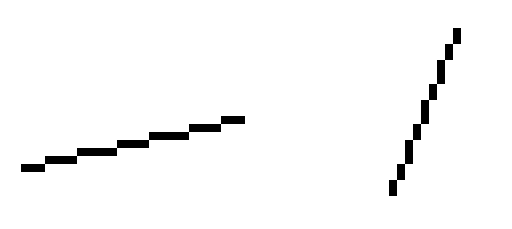
由于电脑显示器的精度有限,我们不可能让直线做到完全平滑,对于非45°角的斜线便会出现不同自变量对应相同因变量的现象,称作“直线走样”。当然为了解决这个问题会有相应的反走样和抗锯齿技术,但不是本节重点,先暂且不提。
首先我们看图1,很显然|△x|>|△y|,选择x为自变量,我们来分析其中的细节部分:
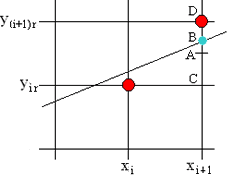
当我们扫描x到了$x_i+1$点时,通过解析式算出的y值并没有落在整数点上(如图的B点),由于屏幕分辨率的限制,我们只能选择在C点或在D点上进行绘制。我们取C和D连线的中点A作为分界,若B的y值大于A则绘制D点,否则绘制C点。
具体算法如下:首先我们规定x的步长为sx=1,y的步长为sy=k(即斜率)。为了方便计算,我们先把y值舍去小数部分取整,这样默认落在了C点上,然后直接取(B的y值)-(A的y值)作为$x_{i+1}$点的偏移量,写作ε($x_{i+1}$)。ε($x_{i+1}$)>0则将y值增加一个像素单位长度,否则不变。公式即为ε($x_{i+1}$)=BC-AC=($y_{i+1}$-$y_{ir}$)-0.5。
为了简化运算,我们可以迭代出ε($x_{i+k}$)的值。
ε($x_{i+2}$)=($y_{i+2}$-$x_{(i+1)r}$)-0.5
=$y_{i+1}$+sy-$y_{(i+1)r}$-0.5
=ε($x_{i+1}$)+$y_{ir}$-$y_{(i+1)r}$
以此类推下去:
ε($x_{i+3}$)=ε($x_{i+2}$)+sy+$y_{(i+1)r}$-$y_{(i+2)r}$
...
ε($x_{i+k}$)=ε($x_{i+k-1}$)+sy+$y_{(i+k-2)r}$-$y_{(i+k-1)r}$
个人认为$y_{(i+k-2)r}$-$y_{(i+k-1)r}$这个式子摆在这里很碍眼,不妨直接分类讨论:
若ε($x_{i+k-1}$)<0,则$y_{(i+k-2)r}$-$y_{(i+k-1)r}$=0:ε($x_{i+k}$)=ε($x_{i+k-1}$)+sy
若ε($x_{i+k-1}$)≥0,则$y_{(i+k-2)r}$-$y_{(i+k-1)r}$=-1:ε($x_{i+k}$)=ε($x_{i+k-1}$)+sy-1
现在递推公式求出来了,基本就可以编程了。但是,事实上我们可以避免浮点运算,只需要进一步优化一下公式。对于起点s而言,有:
①ε($x_{s+1}$)=sy-0.5
②ε($x_{i+k}$)=ε($x_{i+k-1}$)+sy。
③ε($x_{i+k}$)=ε($x_{i+k-1}$)+sy-1。
其中sy和0.5都是讨厌的浮点数,因此我们可以在左右都乘一个2*△x(两个目标点的横坐标差),这样公式也就变成了:
①2*△x*ε($x_{s+1}$)=2*△y-△x
②2*△x*ε($x_{i+k}$)=2*△x*ε($x_{i+k-1}$)+2*△y
③2*△x*ε($x_{i+k}$)=2*△x*ε($x_{i+k-1}$)+2*△y-2*△x
将2*△x*ε统一写成d,则递推式变为
②d=d+2*△y
③d=d+2*△y-2*△x
注意d=2*△x*ε,我们默认△x>0,因此d和ε具有相同的符号。之前我们说当ε≥0时则y值增加,现在我们也可以说d≥0则y值增加。
整理一下,也就是说我们只需要维护一个d值,初始情况下d=2*△y-△x,接下来每次迭代都需要判断一下d的大小,d<0的话则d=d+2*△y;d>0的话则d=d+2*△y-2*△x并且y要增加1个单位,注意每次迭代都要给x++。这部分代码非常简洁,所以我也就不放伪代码了。要注意的是上述我们默认了△x>0,其实存在这样一种情况:x1<x2 y1>y2,此时我们如果取点2为起点的话,就会导致△x<0,这种时候我们就强行把△x取相反数,同时把sx取成-1即可。
最后不要忘了在写入缓冲区的时候,颜色等信息都要取两点之间的插值。因此在传入函数时,我们不能仅仅传入两个坐标,而是要把经过着色器运算的这两个顶点整体传入:
原文:https://www.cnblogs.com/puluomi/p/14604792.html