6-2 在一个数组中实现两个堆栈 (20 分)

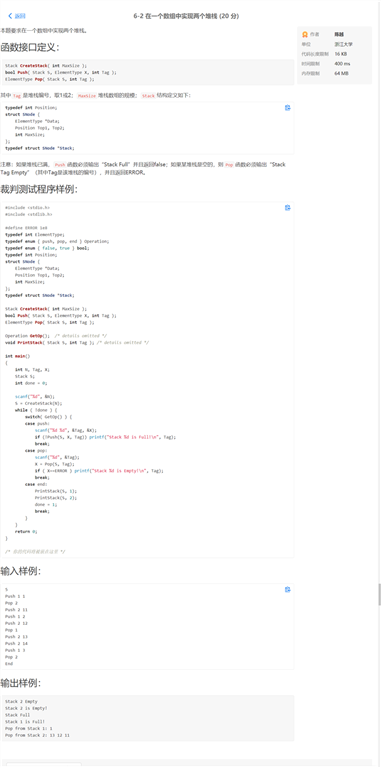
具体解题代码 ：

Stack CreateStack(int MaxSize)
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Data = (ElementType*)malloc(MaxSize * sizeof(ElementType));
    S->Top1 = -1;
    S->Top2 = MaxSize;
    S->MaxSize = MaxSize;
    return S;
}
bool Push(Stack S, ElementType X, int Tag)//入栈
{
    if (S->Top1+1== S->Top2)//栈满
    {
        printf("Stack Full\n");
        return false;
    }
    else
    {
        if (Tag == 1)
        {
            S->Top1++;
            S->Data[S->Top1] = X;
            return true;
        }
        else if (Tag == 2)
        {
            S->Top2--;
            S->Data[S->Top2] = X;
            return true;
        }
    }
}
ElementType Pop(Stack S, int Tag)//出栈
{
    if (Tag == 1)
    {
        if (S->Top1 == -1)//栈空
        {
            printf("Stack %d Empty\n", Tag);
            return ERROR;
        }
        return S->Data[(S->Top1)--];
    }
    else if (Tag == 2)
    {
        if (S->Top2 == S->MaxSize)//栈空
        {
            printf("Stack %d Empty\n", Tag);
            return ERROR;
        }
        return S->Data[(S->Top2)++];
    }
}

解题思路：注意此时top1和top2的初值

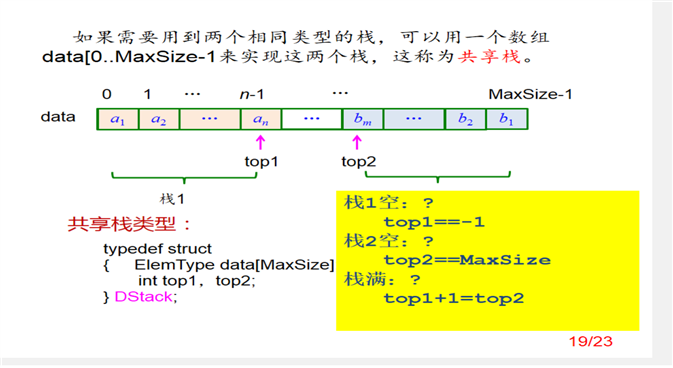
第一部分：Stack CreateStack(int MaxSize)
定义栈1的头指针Top1，栈2的头指针Top2，并且注意定义S->Top1 = -1; S->Top2 = MaxSize;
第二部分：bool Push(Stack S, ElementType X, int Tag)//入栈
1.栈满的条件为Top1+1=Top2，代码为if (S->Top1+1== S->Top2)
2.栈不满时，堆栈编号Tag有两种情况：1和2。当Tag为1时，由图易知，top1需要先往右移动再让X进入此时的位置对应代码为S->Top1++; S->Data[S->Top1] = X;；当Tag为2时，由图易知，需要top2先向左移动，再让x进入此时的位置对应代码为S->Top2--; S->Data[S->Top2] = X;。

第三部分：ElementType Pop(Stack S, int Tag)//出栈
同样的道理，Tag可能为1或2.
当Tag为1时，堆栈为空的条件是此时指针还是指向-1，即初始化的数据；若不为空时，则需要先返回此时数据，在将指针左移。
当Tag为2时，堆栈为空的条件是此时指针还是指向MaxSize，即初始化时的数据。若不为空时，则需要先返回此时数据，再将指针右移。

6-2 在一个数组中实现两个堆栈 (20 分)

原文：https://www.cnblogs.com/whm520/p/14589853.html