欧拉函数:
就是对于一个正整数n,小于n且和n互质的正整数(包括1)的个数,记作φ(n) 。欧拉函数的通式:φ(n)=n*(1-1/p1)(1-1/p2)(1-1/p3)*(1-1/p4)……(1-1/pn),其中p1, p2……pn为n的所有质因数,n是不为0的整数。φ(1)=1(唯一和1互质的数就是1本身)。
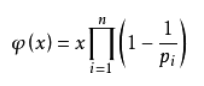
所以,根据通式我们可以打出以下代码:

1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 int main() { 5 int n, ans; 6 cin >> n; 7 ans = n; 8 for (int i = 2; i * i <= n; ++i) 9 if (n % i == 0) 10 { 11 ans = ans / i * (i - 1); 12 while (n % i == 0) 13 n /= i; 14 } 15 if (n > 1) 16 ans = ans / n * (n - 1); 17 cout << ans << endl; 18 return 0; 19 }
原文:https://www.cnblogs.com/geziyu/p/14553698.html