上一节课中,我们讨论了随机响应,这是一种适合于单个位的隐私化。这种算法一般来说并不直接也误差较大。今日所关注的是拉普拉斯机制,可以直接应用于任意一种类型的数字查询。在引入拉普拉斯机制,首先提出一个概念:函数敏感度(sensitivity),一般特指L1敏感度(即基于L1范数的敏感度),定义如下:
使\(f:\mathcal{X}^n\rarr\R ^k\),那么\(f\)的\(\mathcal{l_1}\)-敏感度为:
其中\(X\)和\(X‘\)为邻近数据集
后面丢掉\(f\),只使用\(\Delta\)以表示\(\mathcal{l_1}\)-敏感度。
敏感度用于衡量差分隐私的内容是合适而自然的,正因为差分隐私试图掩盖一个个个体的具体分布差距,通过这一敏感度作为上界,就可以衡量该函数应该会发生多大的改变。值得注意的是,我们用的是\(\mathcal{l_1}\)-敏感度,而非\(\mathcal{l_2}\)-敏感度,但是在其他分布例如说高斯机制中会使用。举个例子:\(f=\frac{1}{n}\sum^n_{i=1}X_i \ \ X_i\in\{0,1\}\),很容易算出敏感度为\(1/n\),因为只有一个位被翻转。
对于位置与规模参数分别为\(0\)与\(b\)的拉普拉斯分布,如下定义其密度函数:
注意到拉普拉斯分布的方差为\(2b^2\)。
如下图所示,拉普拉斯分布本质是两个对称的指数分布,在\(x\in [0,\infty)\)存在正比于\(exp(-cx)\)的密度函数,而拉普拉斯分布则是在\(x\in \R\)存在正比于\(\exp(-c|x|)\)的密度函数。另外高斯分布的尾部要比拉普拉斯分布的稍轻一点,换句话来说就是高斯分布的中心化程度更高。
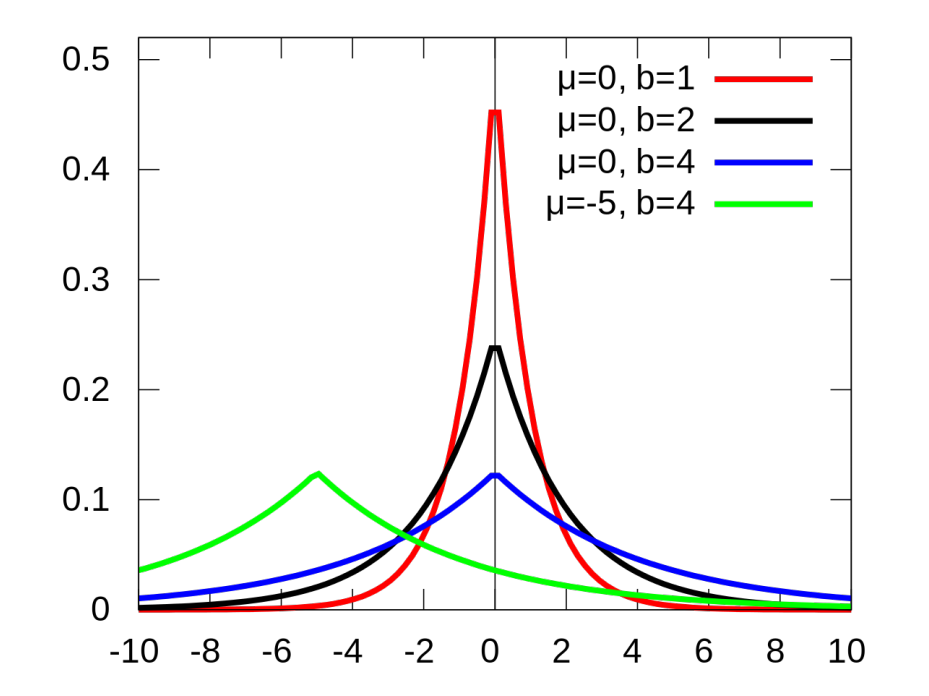
介绍了拉普拉斯分布之后,就可以引入拉普拉斯机制这一概念,原理非常简单:即是按照数据敏感度的程度添加噪音。
使\(f:\mathcal{X}^n\rarr\R ^k\),那么拉普拉斯机制即是
其中\(Y_i\)是独立的拉普拉斯分布,\(Laplace(\Delta/\epsilon)\)的随机变量。
由此我们就可以将其应用于例子中的\(f=\frac{1}{n}\sum^n_{i=1}X_i\),并且\(k=1\)。那么\(\Delta = 1/n\)。为此,对其施加拉普拉机制之后得到\(\tilde p=f(X)+Y\),其中\(Y\)为\(Laplace(1/(\epsilon n))\)。由定义可知,\(\mathbf{E}[\tilde p]=p\),\(\mathbf{Var}[\tilde p]=\mathbf{Var}[Y]=O(1/(\epsilon^2 n^2))\),然后通过切比雪夫不等式就可以得到合理概率界限。对比于\(\epsilon\)-随机响应的精确度\(O(1/(\epsilon\sqrt n))\),可见拉普拉斯机制是二次的,小于\(\epsilon\)-随机响应。
拉普拉斯机制乃是\(\epsilon\)-差分隐私
证明:假若\(X\)与\(Y\)为一对邻近数据集,存在一个数据条目不一致。使得\(p_X(z)\)与\(p_y(z)\)为点\(z\in\R^k\)的概率密度函数\(M(X)\)与\(M(Y)\)。为此我们需要证明其上界为\(\exp(\epsilon)\),那么对于任意一个\(X\)与\(Y\)的\(z\)
首先应用三角不等式,然后应用\(\mathcal{l_1}\)-敏感度的定义。
数据挖掘 | 数据隐私(4) | 差分隐私 | 差分隐私概论(下)(Intro to Differential Privacy 2)(未完)
原文:https://www.cnblogs.com/uzuki/p/14496440.html