| # matlab实验 |
|---|
| ## 第一次课实验题目 |
| ### 第1题 |
| 计算如下表达式: |
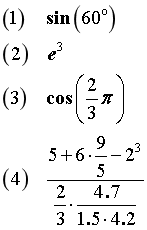 |
(1) |
(2) |
(3) 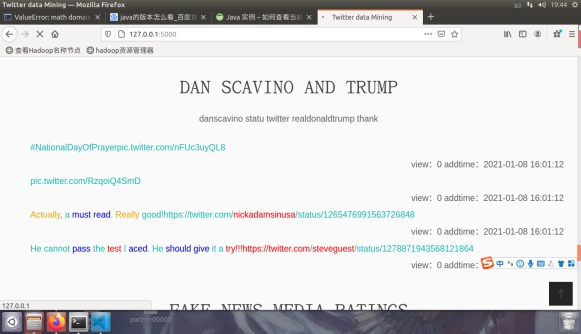 |
(4) 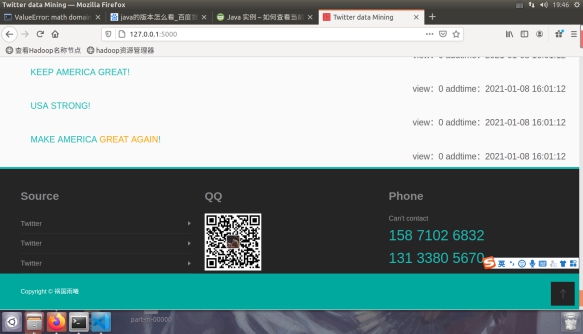 |
| ### 第2题 |
| 求出下式中矩阵z的值: |
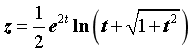 ,其中 ,其中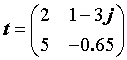 |
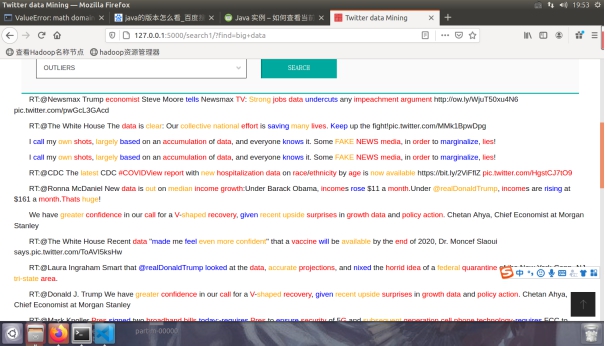 |
| ### 第3题 |
已知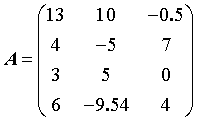 , , |
| 1) 取出*A**的第2、4、8、12、10、9个元素构成一个新的矩阵*A***1*,其中*A*****的第2、4个元素构成新矩阵的第一行,第8、12个元素构成新矩阵的第二行,第10、9个元素构成新矩阵的第三行; |
| 2) 将*A***1*的所有元素构成一个行向量*A*****2*。 |
 |
 |
 |
| ### 第4题 |
已知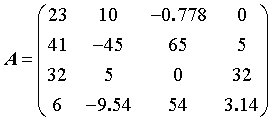 , , |
| 取出*A**的前三行构成矩阵*B**,其前两列构成矩阵*C*,其右下角的3×2子矩阵构成矩阵*D*,*B*与*C*的乘积构成*E***,分别给出各个矩阵。 |
 |
 |
 |
 |
 |
| ### 第5题 |
| 已知,,求下列表达式的值: |
| 1) 、(其中I为单位阵); |
| 2) 、、、; |
| 3) 、、、; |
| (1) |
|  |
| (2)  |
|  |
|  |
|  |
(3) 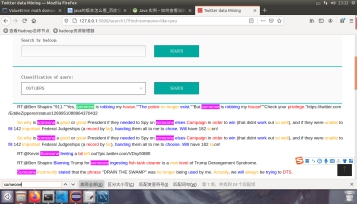 |
| ### 第6题 |
| 产生均值为3,方差为1的5阶正态分布的随机方阵。 |
|  |
|  |
| ### 第7题 |
| 求解下列联立方程的解: |
|  |
|  |
| ### 第8题 |
| 建立一个字符串向量,要求字符串向量中至少包含自己的姓名和生日,姓名中首字母均为大写,其余字母没有要求。 |
| (1) 随机取 2~6 个字符组成子字符串。 |
|  |
| (2) 分别取第偶数个字符组成子字符串1,取第奇数个字符组成子字符串2,比较两个字符串的异同。 |
|  |
| #### 修改 |
| ```matlab |
| str1=str(round(int8(rand(1,int8(rand(1,1)4+2))11+1))) |
| ``` |
| (3) 取出里面的数字并转化为数值,然后求和。(选做) |
|  |
| (4) 去掉字符串中的数字字符。(选做) |
|  |
| (5)将字符串按照倒序重新排列。 |
|  |
| (5) 将字符串中的小写字母变成大写字母,其他不变。(选做) |
| (6)  |
| (7)统计字符串中消息字母的个数。(即字符串中的空格不算在内) |
|  |
| ### 第9题 |
| 逆公式。 |
| 使用符号计算的方法得到3阶方阵的矩阵求逆公式。 |
|  |
| ans = |
| [ (a22a33 - a23a32)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), (a12a32 - a12a33)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), -(a12a22 - a12a23)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31)] |
| [ -(a21a33 - a23a31)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), -(a12a31 - a11a33)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), (a12a21 - a11a23)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31)] |
| [ (a21a32 - a22a31)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), -(a11a32 - a12a31)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31), (a11a22 - a12a21)/(a12a21a32 - a12a22a31 + a11a22a33 - a11a23a32 - a12a21a33 + a12a23a31)] |
| ### 第10题 |
| 用符号计算指令symsum求1+x+x2+...+xk的求和公式。 |
| (使用F1获得帮助文件,学习symsum的用法) |
|  |
| ## 第二次课实验题目 |
| ### 第一题 |
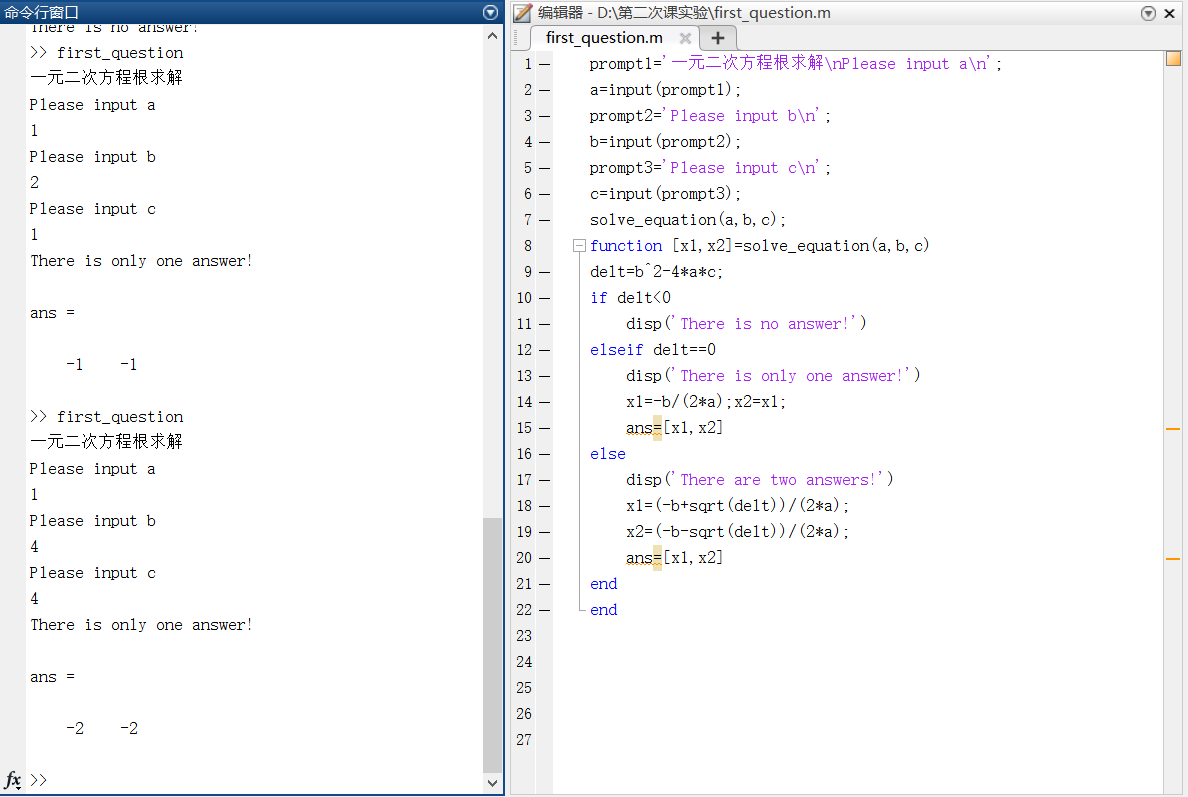 |
| ```matlab |
| prompt1=‘一元二次方程根求解\nPlease input a\n‘; |
| a=input(prompt1); |
| prompt2=‘Please input b\n‘; |
| b=input(prompt2); |
| prompt3=‘Please input c\n‘; |
| c=input(prompt3); |
| solve_equation(a,b,c); |
| function [x1,x2]=solve_equation(a,b,c) |
| delt=b^2-4ac; |
| if delt<0 |
| disp(‘There is no answer!‘) |
| elseif delt==0 |
| disp(‘There is only one answer!‘) |
| x1=-b/(2*a);x2=x1; |
| ans=[x1,x2] |
| else |
| disp(‘There are two answers!‘) |
| x1=(-b+sqrt(delt))/(2*a); |
| x2=(-b-sqrt(delt))/(2*a); |
| ans=[x1,x2] |
| end |
| end |
| ``` |
| ### 第二题 |
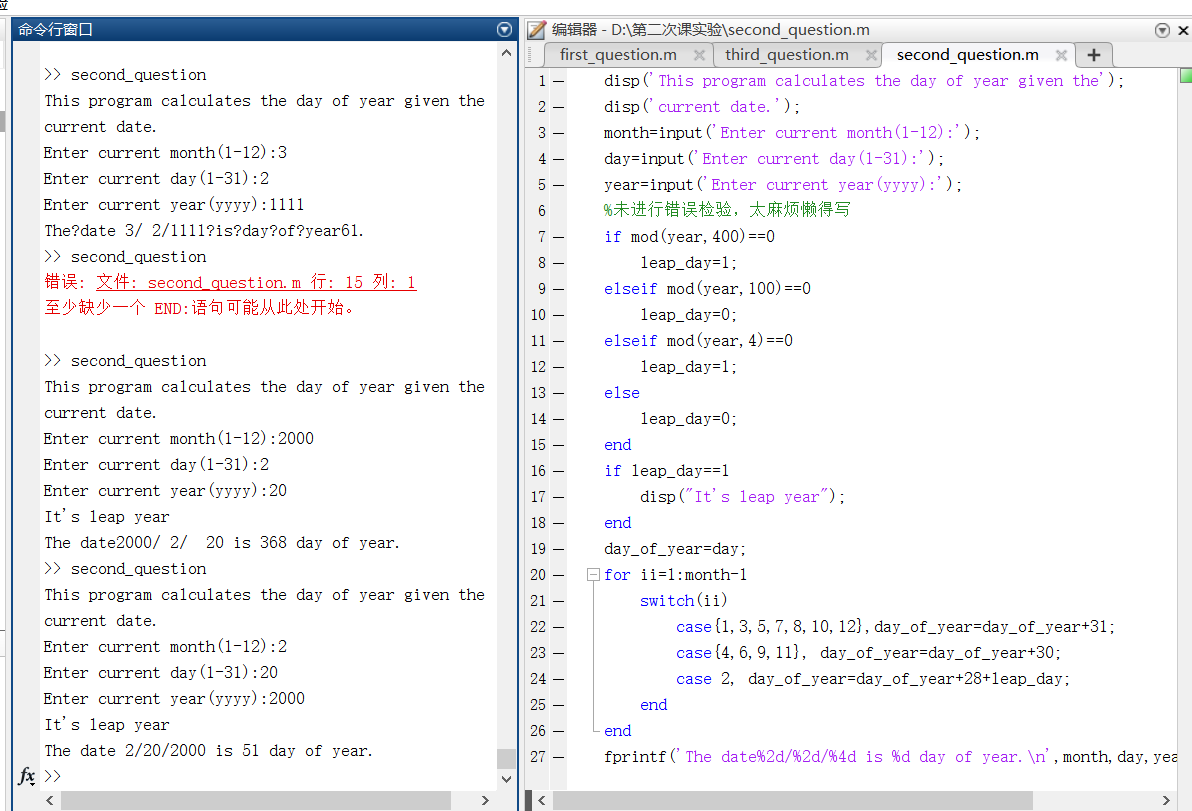 |
| ```matlab |
| disp(‘This program calculates the day of year given the‘); |
| disp(‘current date.‘); |
| month=input(‘Enter current month(1-12)??; |
| day=input(‘Enter current day(1-31)??; |
| year=input(‘Enter current year(yyyy)??; |
| %未进行错误检验,太麻烦懒得写 |
| if mod(year,400)==0 |
| leap_day=1; |
| elseif mod(year,100)==0 |
| leap_day=0; |
| elseif mod(year,4)==0 |
| leap_day=1; |
| else |
| leap_day=0; |
| end |
| if leap_day==1 |
| disp("It‘s leap year"); |
| end |
| day_of_year=day; |
| for ii=1:month-1 |
| switch(ii) |
| case{1,3,5,7,8,10,12},day_of_year=day_of_year+31; |
| case{4,6,9,11}, day_of_year=day_of_year+30; |
| case 2, day_of_year=day_of_year+28+leap_day; |
| end |
| end |
| fprintf(‘The date%2d/%2d/%4d is %d day of year.\n‘,month,day,year,day_of_year); |
| ``` |
| ### 第三题 |
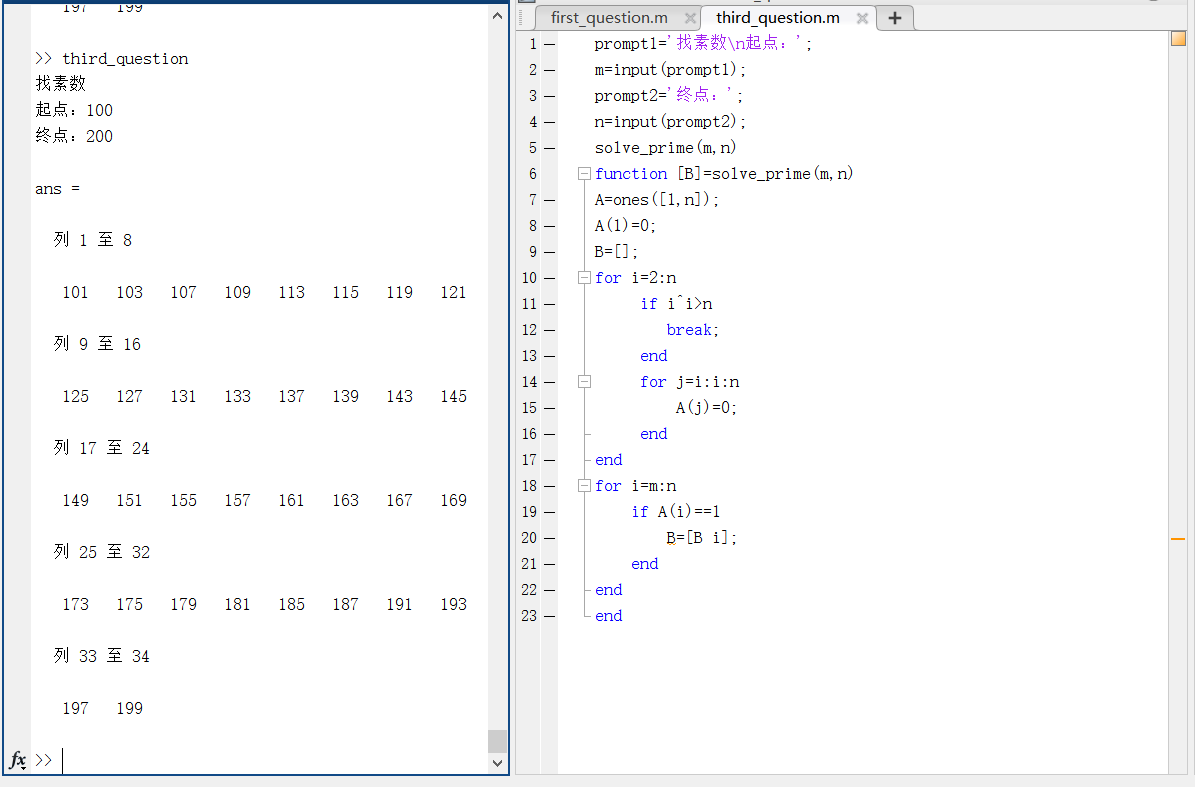 |
| ```matlab |
| prompt1=‘找素数\n起点:‘; |
| m=input(prompt1); |
| prompt2=‘终点:‘; |
| n=input(prompt2); |
| solve_prime(m,n) |
| function [B]=solve_prime(m,n) |
| %找到从起点到终点之间的所有素数 |
| A=ones([1,n]); |
| A(1)=0; |
| B=[]; |
| for i=2:n |
| if i^i>n |
| break; |
| end |
| for j=i:i:n |
| A(j)=0; |
| end |
| end |
| for i=m:n |
| if A(i)==1 |
| B=[B i]; |
| end |
| end |
| end |
| ``` |
| #### 优化 |
| ``` |
| prompt1=‘找素数\n起点:‘; |
| m=input(prompt1); |
| prompt2=‘终点:‘; |
| n=input(prompt2); |
| solve_prime(m,n) |
| function [B]=solve_prime(m,n) |
| %找到从起点到终点之间的所有素数 |
| A=ones([1,n]); |
| A(1)=0; |
| B=[]; |
| for i=2:m |
| if i^i>n |
| break; |
| end |
| if A(i)==1 |
| for j=i:i:n |
| A(j)=0; |
| end |
| end |
| end |
| for i=m:n |
| if A(i)==1 |
| B=[B i]; |
| end |
| end |
| end |
| ``` |
| ### 第四题 |
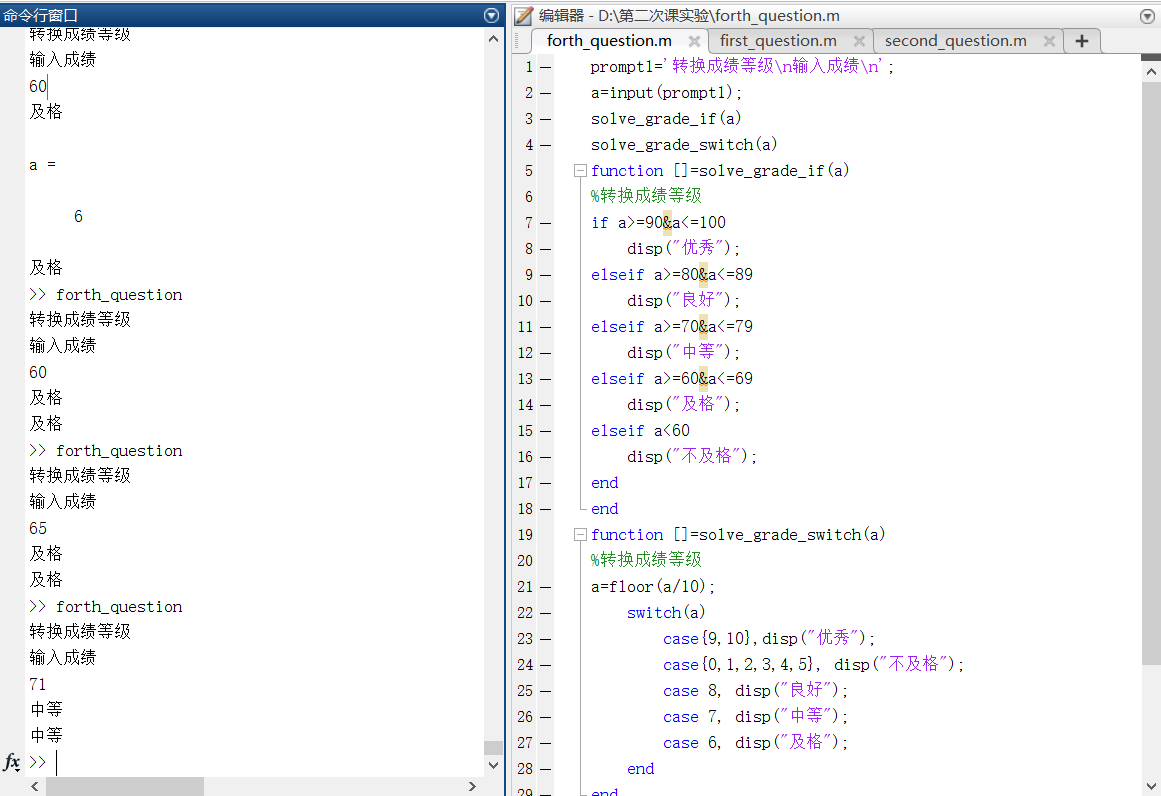 |
| ```matlab |
| prompt1=‘转换成绩等级\n输入成绩\n‘; |
| a=input(prompt1); |
| solve_grade_if(a) |
| solve_grade_switch(a) |
| function []=solve_grade_if(a) |
| %转换成绩等级 |
| if a>=90&a<=100 |
| disp("优秀"); |
| elseif a>=80&a<=89 |
| disp("良好"); |
| elseif a>=70&a<=79 |
| disp("中等"); |
| elseif a>=60&a<=69 |
| disp("及格"); |
| elseif a<60 |
| disp("不及格"); |
| end |
| end |
| function []=solve_grade_switch(a) |
| %转换成绩等级 |
| a=floor(a/10); |
| switch(a) |
| case{9,10},disp("优秀"); |
| case{0,1,2,3,4,5}, disp("不及格"); |
| case 8, disp("良好"); |
| case 7, disp("中等"); |
| case 6, disp("及格"); |
| end |
| end |
| ``` |
| ### 第五题 |
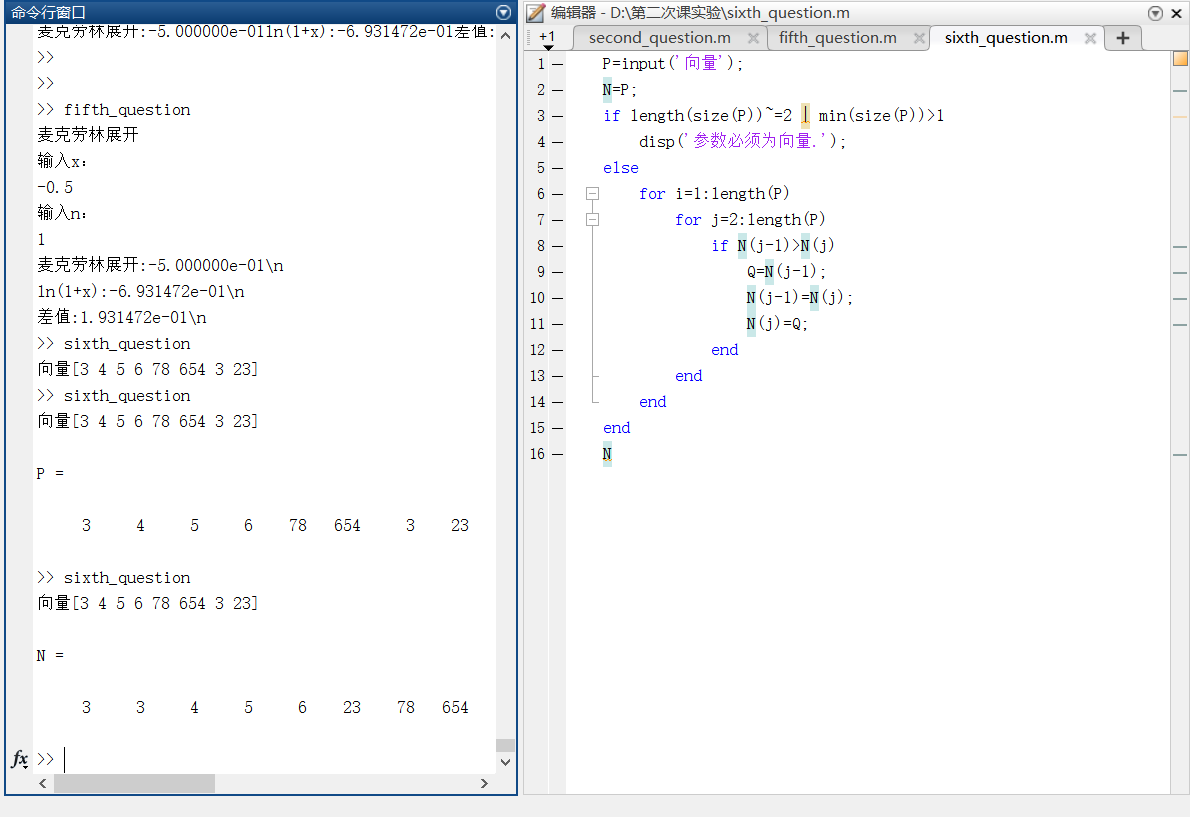 |
| ```matlab |
| prompt1=‘麦克劳林展开\n输入x:\n‘; |
| x=input(prompt1); |
| prompt2=‘输入n:\n‘; |
| n=input(prompt2); |
| fprintf(‘麦克劳林展开:%s‘,solve_function(x,n)); |
| disp(‘\n‘) |
| fprintf("ln(1+x):%s",solve_ln(x)); |
| disp(‘\n‘) |
| fprintf("差值:%s",abs(solve_function(x,n)-solve_ln(x))); |
| disp(‘\n‘) |
| function [ans]=solve_function(x,n) |
| ans=0; |
| for i=1:n |
| ans=ans+(-1)(i+1)*x(i)/i; |
| end |
| end |
| function [ans]=solve_ln(x) |
| ans=log(1+x); |
| end |
| ``` |
| ### 第六题 |
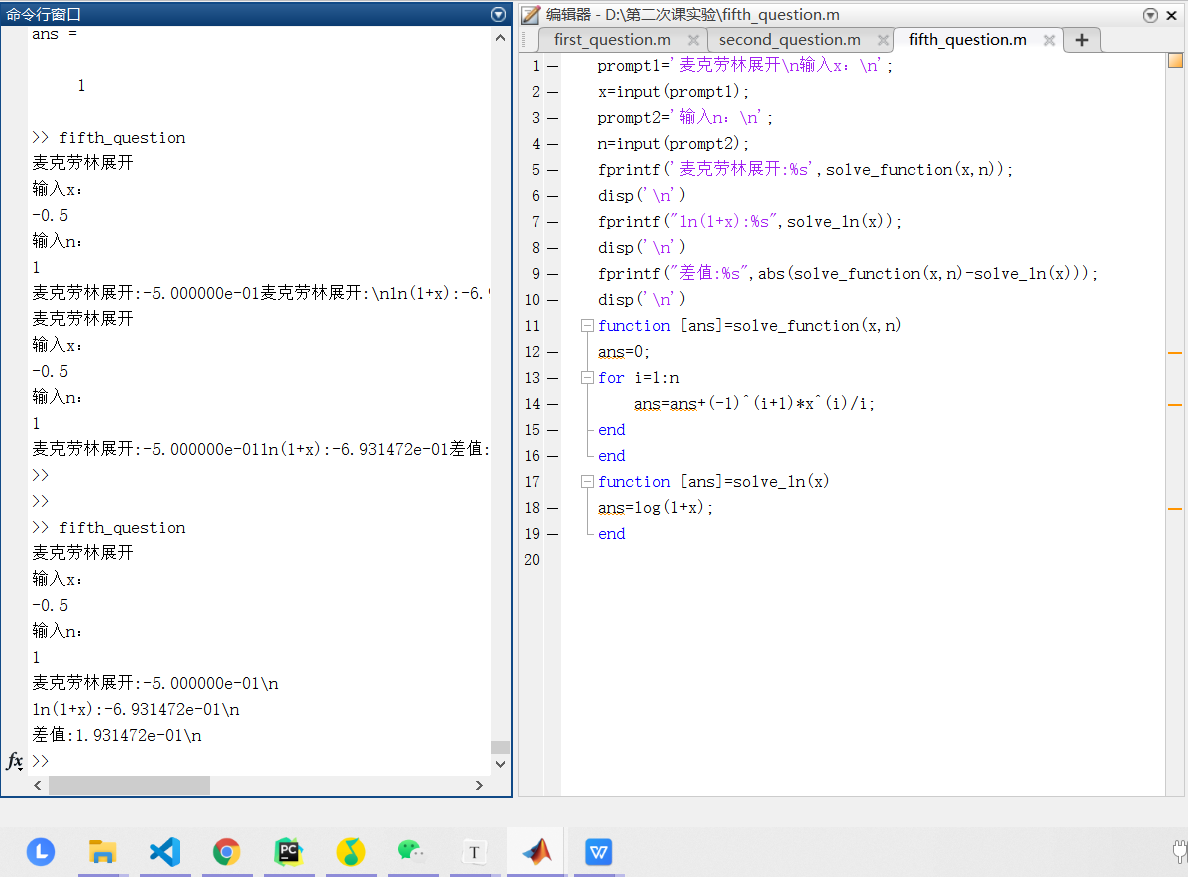 |
| ```matlab |
| P=input(‘向量‘); |
| N=P; |
| if length(size(P))~=2 |
| disp(‘参数必须为向量.‘); |
| else |
| for i=1:length(P) |
| for j=2:length(P) |
| if N(j-1)>N(j) |
| Q=N(j-1); |
| N(j-1)=N(j); |
| N(j)=Q; |
| end |
| end |
| end |
| end |
| N |
| ``` |
| #### 优化 |
| ```matlab |
| P=input(‘向量‘); |
| N=P; |
| if length(size(P))~=2 |
| disp(‘参数必须为向量.‘); |
| else |
| for i=1:length(P) |
| flag=1;%增加flag位,当一次冒泡不再交换时跳出 |
| for j=2:length(P) |
| if N(j-1)>N(j) |
| Q=N(j-1); |
| N(j-1)=N(j); |
| N(j)=Q; |
| flag=0; |
| end |
| end |
| if flag==1 |
| break |
| end |
| end |
| end |
| N |
| ``` |
原文:https://www.cnblogs.com/huoguoyuxi/p/14495955.html