力扣刷题记录2021.3.4 回溯算法 组合问题

B站一个up主总结的回溯算法的模板

void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表); // 递归
回溯，撤销处理结果
}
}

实际上回溯算法就是树形结构，然后遍历整个树，重点就是需要回溯，这是一个组合问题的树形结构

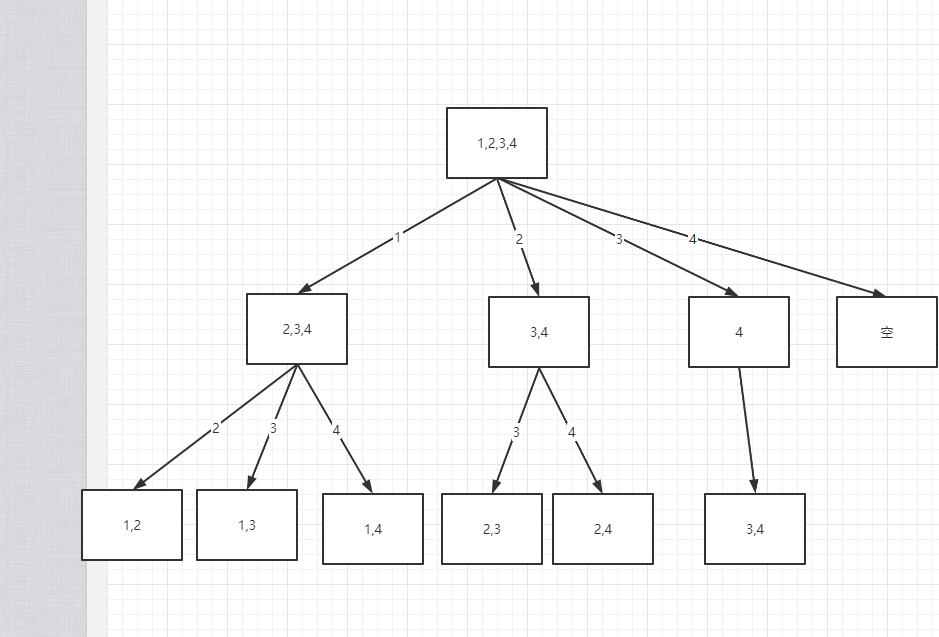
 回溯算法可以解决很多问题 比如 组合问题 排列问题 切割问题 子集问题等

题目描述：

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

在组合问题中，关键参数就是就是数据集n，组合大小数k，搜索起点 begin，用来记录路径的path，结果集res

思路就是从begin开始遍历，一直遍历到n，将遍历的元素添加到路径path中，如果深度等于k时，就将path添加到结果集，

具体代码：

public class combinationProblem {

    public static void main(String[] args) {
        combinationProblem combinationProblem = new combinationProblem();
        System.out.println(combinationProblem.combine(5, 2));
    }

    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        // 从 1 开始是题目的设定
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        // 递归终止条件是：path 的长度等于 k,实际上就是叶子节点，我们需要在这里收集结果
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 遍历可能的搜索起点
        for (int i = begin; i <= n; i++) {
            // 向路径变量里添加一个数
            path.addLast(i);
            System.out.println(path);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
            dfs(n, k, i + 1, path, res);
            // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
            //path.pop();  //pop和removelist一样
            //这里就是回溯的过程,弹出最后一个元素
            path.removeLast();
        }
    }
}

来查看一下每一步的path 和最后的 res

path：

[1]
[1, 2]
[1, 3]
[1, 4]
[1, 5]
[2]
[2, 3]
[2, 4]
[2, 5]
[3]
[3, 4]
[3, 5]
[4]
[4, 5]
[5]

res：
[[1, 2], [1, 3], [1, 4], [1, 5], [2, 3], [2, 4], [2, 5], [3, 4], [3, 5], [4, 5]]

可以更好的理解回溯算法的整个过程

力扣刷题记录2021.3.4 回溯算法 组合问题

原文：https://www.cnblogs.com/spx88/p/14479456.html