排序算法的实用意义还是很高的,可应用在商业处理,语音识别,天体物理学等领域。本文对简单排序(选择排序,插入排序,希尔排序)的几个模型做一些总结。
遵循Java的规范,可以使用Comparable接口强行对实现它的类的每个实例进行自然排序。当然使用其他语言可以不需要遵循这个规范使用Comparable可以很好的执行less()对元素进行比较和exch()完成元素的交换。
方法:int compareTo(Object o)
利用当前对象和传入的目标对象进行比较,
Comparable接口强行对实现它的类的每个实例进行自然排序,该接口的唯一方法compareTo方法被称为自然比较方法;强烈建议自然排序和equals一致(就是两个对象调用compareTo方法和调用equals方法返回的布尔值应该一样)。
在这里对一些调用做一些说明算法说明:
//交换元素
private static void exch(Comparable[] a,int i,int j)
{
Comparable t=a[i];a[i]=a[j];a[j]=t;
}
//比较
private static boolean less(Comparable[] v,Comparable[] w)
{
return v.compareTo(w)<0;
}
选择排序是最简单的一类排序(简言之就是从数组中选择最小或者最大的元素进行排序):
public class Selection
{ //将a[]按升序排列
public static void sort(Comparable[] a)
{
int N=a.length;
//内循环进行比较以及交换
for(int i=0;i<N;i++)
{
int min=i;
for(int j=i+1;j<N;j++)
{
if(less(a[j]),a[min])
min=j;
exch(a,i,min);
}
}
}
}
成本分析:
选择排序特点总结
1.运行时间与输入无关
内循环循环结束之后都不会对下一组循环造成影响,也就是为了找到当前最小元素而扫描一遍数组并不能为下一遍扫描提供什么信息。
这样对一个有序数组和元素全部相等的数组和一个元素进行排序所用时间相同。
2. 数据移动是最少的
交换数据的次数与数组大小是线性关系。(其他大部分算法都是线性对数或者平方级别)
插入排序的执行过程如下:
每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插完所有元素为止。执行示例如下: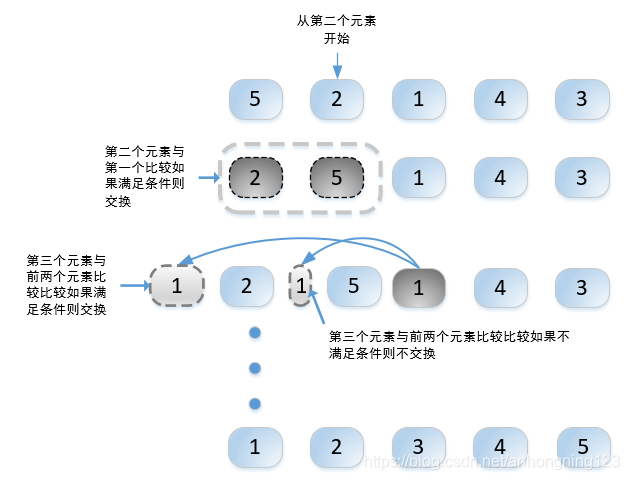
public class Insertion
{
public static void sort(Comparable[] a)
{
//将a[]按升序排列
int N=a.length;
for (int i=1;i<N;i++)
{//执行插入过程判断条件满足两个要求:
// 1.遍历完当前元素左侧所有元素
//2.前一个元素大于当前元素(类似冒泡后续会展开)
for(int j=i;j>0&&less(a[j],a[j-1]);j--)
{
exch(a,j,j-1);
}
}
}
}
在这里对插入排序的运行规模做一个总结:
具有N个元素的随机排列(元素不重复),平均情况下需要$N{2}/4$次比较,$N{2}/4$次交换。
(最坏情况下有$N{2}/2$次比较,$N{2}/2$次交换,最好情况下需要$N-1$次比较与$0$次交换)。
这里注意一点插入排序会受输入的数组影响。
例如:如果输入的数组是有序的,这时候插入一个元素能够很容易找到需要插入的位置,这时运行时间是线性的(对于选择排序是平方级别的)
与选择排序相比:
这里给出一个有关倒置的推论(读者理解交换即可)
插入排序需要的交换操作和数组中倒置的数量相同,需要比较的次数大于等于倒置的数量。小于等于数组的数量加上倒置的数量减一
其实不难理解,交换的目的就是消除倒置(敲重点啦!!)每个元素回到应有的顺序就消除一个倒置,倒置数量为0时也就相当于排序完成。
但是1~N-1每个i元素都可能有多一次比较因为当前元素还没有到达对应的位置(左端)。
希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序其实也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破$N^{2}$的第一批算法之一。
希尔排序的思想其实是一种分组插入的方法
希尔排序的目标是使数组中间任意间隔h的元素有序。其中每隔h的元素组成h有序数组。一个h有序数组就是由h个有序子数列组成的数组
例如:
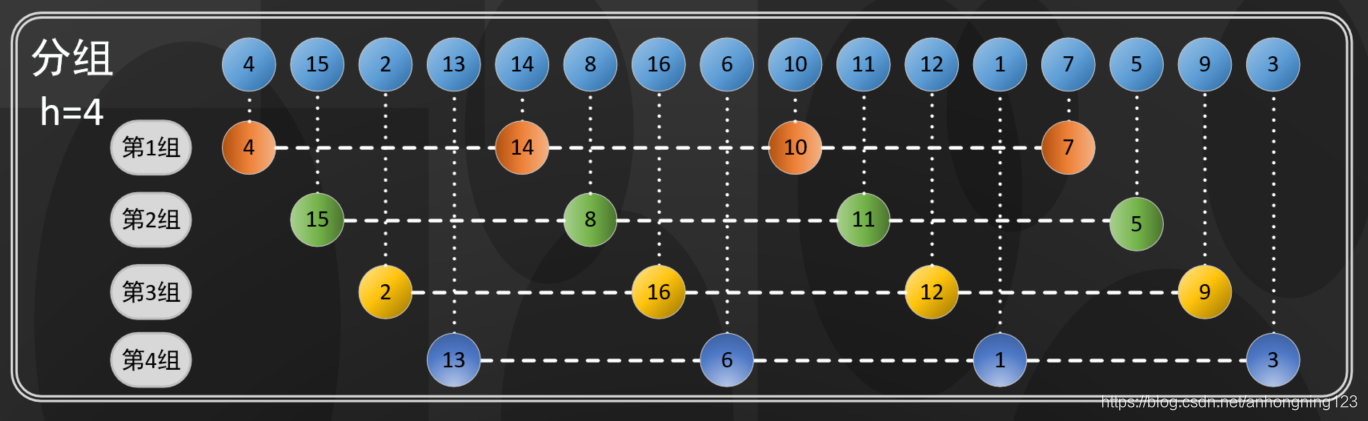
一个长度为16的数组,h=4时如下图:
上图中每隔4个元素分组,每个分组由4个元素构成,一个4-有序数组
一个长度为16的数组,h=5时如下图:
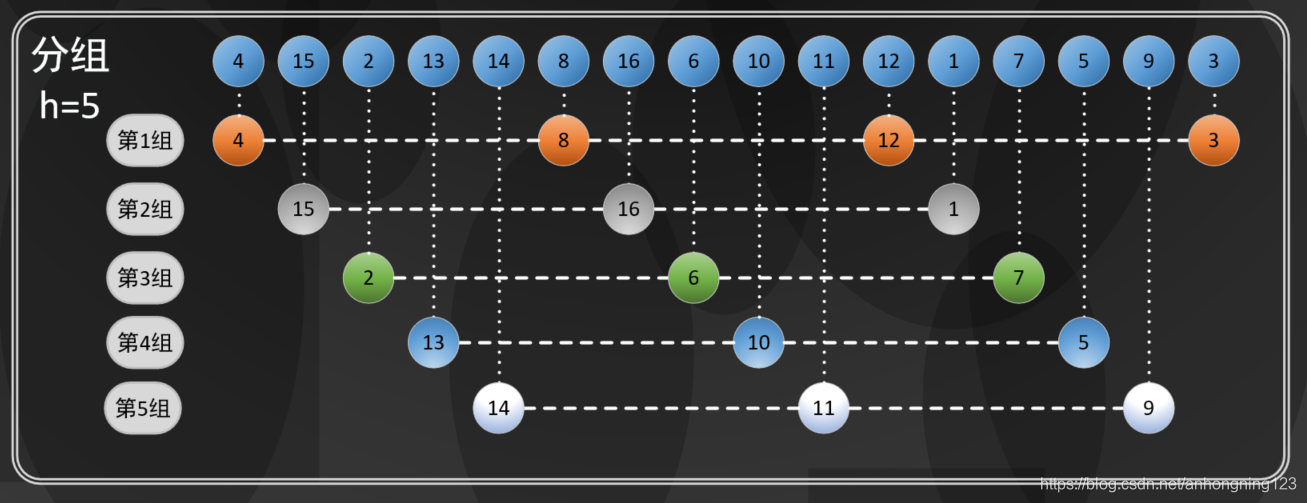
上图中每隔5个元素分组,一个5-有序数组
为了方便读者理解,以下给出希尔排序的图解,如下(可以单击放大查看):
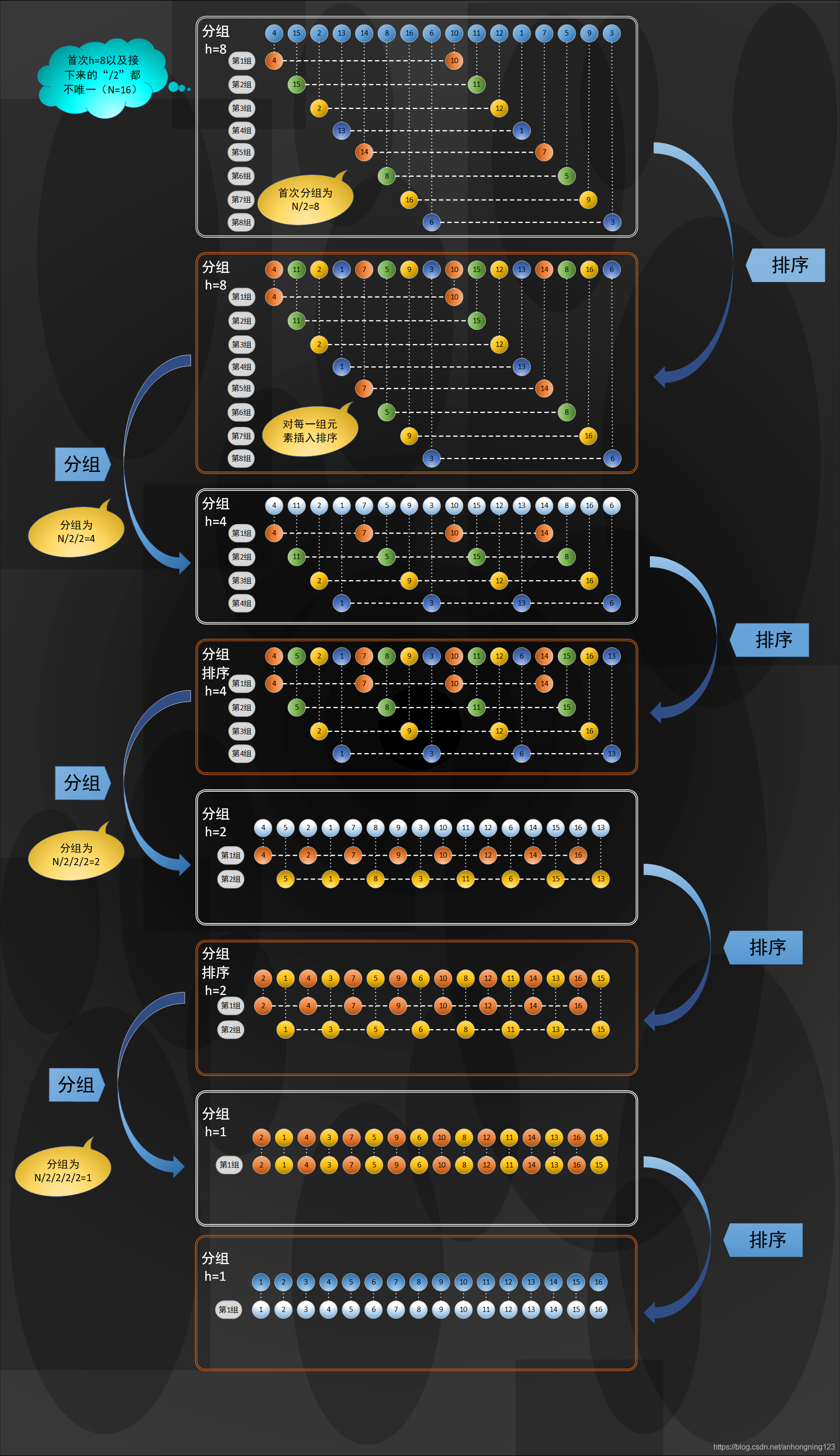
代码如下,
public class Shell
{
public static void sort(Comparable[] a)
{
int N=a.length;
int h=N/2;
while(h>=1)
{
//获取h的长度,首先从N/2开始
for (int i=h;i<N;i++)
{
//对各个分组进行插入排序
for(int j=i;j>=0&&less(a[j],a[j-h]);j-=h)
{
exch(a,j,j-h);//用法见本章接口说明
}
}
h=h/2;
}
}
}
希尔排序的复杂度和递增序列是相关的,算法的性能不仅仅取决于h,还取决于h之间的数学性质,比如分组为(4,2,1)或者分组为(9,3,1)。所以很难去描述其对乱序的数组性能特征的排序方法。针对不同的递增序列序列会有不同的时间复杂度。
希尔排序对中等大小的数组还是具有很好的性能的,代码量小,并且不需要额外空间。对于不要求极端的运行环境情况下是一个不错的选择。| | | |
| ---- | ---- | ---- |
| | | || | | |
| ---- | ---- | ---- |
| | | || | | |
| ---- | ---- | ---- |
| | | || | | |
| ---- | ---- | ---- |
| | | |
原文:https://www.cnblogs.com/suanfawu/p/14442232.html