1.传统DNN的反向传播计算:
损失函数: \(J(W,b,x,y) = \cfrac{1}{2}||a^L-y||_2^2\)
\[\delta^l=\frac {\partial J}{\partial z^l} \,\,\text{表示对l层线性变换输出$z^l$的偏导}
\]
最后一层输出层: \(\cfrac {\partial J}{\partial a^L} = a^L - y\)
\[z^L=W^L a^{L-1} +b^L\\,\dZL=\delta^L = \cfrac{\partial J(W,b,x,y)}{\partial z^L} = \cfrac{\partial J(W,b,x,y)}{\partial a^L}\odot \sigma^{‘}(z^L)=(a^L-y)\odot\sigma‘(z^L)
\\,\dWL = \cfrac{\partial J(W,b,x,y)}{\partial W^L}=\cfrac{\partial J(W,b,x,y)}{\partial z^L}\cfrac{\partial z^L}{\partial W^L}=\delta^L(a^{L-1})^T\\\,\dbL=\delta^L
\]
第l层:
\[dZl=\delta^{l} = \cfrac{\partial J(W,b,x,y)}{\partial z^l} = (\cfrac{\partial z^{l+1}}{\partial z^{l}})^T\cfrac{\partial J(W,b,x,y)}{\partial z^{l+1}} =(\cfrac{\partial z^{l+1}}{\partial z^{l}})^T \delta^{l+1}=(W^{l+1})^T\delta^{l+1}\odot\sigma‘(z^l)\\\,\dWl=\delta^l(a^{l-1})^T\\\,\dbl=\delta^l
\]
2. CNN的反向传播算法思想
要套用DNN的反向传播算法到CNN,有几个问题需要解决:
1)池化层没有激活函数,这个问题倒比较好解决,我们可以令池化层的激活函数为\(σ(z)=z\),即激活后就是自己本身。这样池化层激活函数的导数为1.
2)池化层在前向传播的时候,对输入进行了压缩,那么我们现在需要向前反向推导 \(\delta^{l-1}\),这个推导方法和DNN完全不同。
3) 卷积层是通过张量卷积,或者说若干个矩阵卷积求和而得的当前层的输出,这和DNN很不相同,DNN的全连接层是直接进行矩阵乘法得到当前层的输出。这样在卷积层反向传播的时候,上一层的 \(\delta^{l-1}\)递推计算方法肯定有所不同。
4)对于卷积层,由于 \(W\) 使用的运算是卷积,那么从\(\delta^l\)推导出该层的所有卷积核的W,b的方式也不同。
从上面可以看出,问题1比较好解决,但是问题2,3,4就需要好好的动一番脑筋了,而问题2,3,4也是解决CNN反向传播算法的关键所在。另外大家要注意到的是,DNN中的al,zlal,zl都只是一个向量,而我们CNN中的al,zl都是一个张量,这个张量是三维的,即由若干个输入的子矩阵组成。
下面我们就针对问题2,3,4来一步步研究CNN的反向传播算法。
在研究过程中,需要注意的是,由于卷积层可以有多个卷积核,各个卷积核的处理方法是完全相同且独立的,为了简化算法公式的复杂度,我们下面提到卷积核都是卷积层中若干卷积核中的一个。
3. 已知池化层的\(\delta^l\),推导上一隐藏层的\(\delta^{l-1}\)
我们首先解决上面的问题2,如果已知池化层的\(\delta^l\),推导出上一隐藏层的\(\delta^{l-1}\)。
在前向传播算法时,池化层一般我们会用MAX或者Average对输入进行池化,池化的区域大小已知。现在我们反过来,要从缩小后(Pooling后)的误差\(\delta^l\),还原前一次较大区域对应的误差。
池化操作介绍
所谓的池化,就是对图片进行降采样,最大池化就是在图片中用每个区域的最大值代表这个区域,平均池化就是用每个区域平均值代表这个区域。

池化层反向传播
池化层的反向传播比较容易理解,我们以最大池化举例,上图中,池化后的数字6对应于池化前的红色区域,实际上只有红色区域中最大值数字6对池化后的结果有影响,权重为1,而其它的数字对池化后的结果影响都为0。假设池化后数字6的位置delta误差为 δ,误差反向传播回去时,红色区域中最大值对应的位置delta误差即等于 δ,不仅要记录区域的最大值,同时也要记录下来区域最大值的位置,方便delta误差的反向传播。
因此,在卷积神经网络最大池化前向传播时,不仅要记录区域的最大值,同时也要记录下来区域最大值的位置,方便delta误差的反向传播。
而平均池化就更简单了,由于平均池化时,区域中每个值对池化后结果贡献的权重都为区域大小的倒数,所以delta误差反向传播回来时,在区域每个位置的delta误差都为池化后delta误差除以区域的大小。
在反向传播时,我们首先会把\(\delta^l\)的所有子矩阵矩阵大小还原成池化之前的大小,然后如果是MAX,则把\(\delta^l\)的所有子矩阵的各个池化局域的值放在之前做前向传播算法得到最大值的位置。如果是Average,则把\(\delta^l\)的所有子矩阵的各个池化局域的值取平均后放在还原后的子矩阵位置。这个过程一般叫做upsample。
\[\delta_k^{l-1} = (\frac{\partial a_k^{l-1}}{\partial z_k^{l-1}})^T\frac{\partial J(W,b)}{\partial a_k^{l-1}} = upsample(\delta_k^l) \odot \sigma^{‘}(z_k^{l-1})\\\,\\delta^{l-1} = upsample(\delta^l) \odot \sigma^{‘}(z^{l-1})
\\\,\\text{由 1)一般pooling时 $\sigma(z)$ = z , $\sigma‘(z)$ = 1}
\]
4.已知卷积层的\(\delta^{l}\),推导上一隐藏层的\(\delta^{l-1}\)
对于卷积层的反向传播,我们首先回忆下卷积层的前向传播公式:
\[a^l= \sigma(z^l) = \sigma(a^{l-1}*W^l +b^l)\text{ ( * 表示 卷积)}
\]
其中 \(n\_in\) 为上一隐藏层的输入子矩阵个数。
在DNN中,我们知道\(\delta^{l-1}\)和$\delta^{l} $的递推关系为:
\[\delta^{l} = \frac{\partial J(W,b)}{\partial z^l} =(\frac{\partial z^{l+1}}{\partial z^{l}})^T \frac{\partial J(W,b)}{\partial z^{l+1}} =(\frac{\partial z^{l+1}}{\partial z^{l}})^T\delta^{l+1}
\]
因此要推导出\(\delta^{l-1}\)和\(\delta^{l}\)的递推关系,必须计算\(\cfrac{\partial z^{l}}{\partial z^{l-1}}\)的梯度表达式。
注意到\(z^{l-1}\)和\(z^{l}\)的关系为:
\[z^l = a^{l-1}*W^l +b^l =\sigma(z^{l-1})*W^l +b^l
\]
因此我们有:
\[\delta^{l-1} = (\frac{\partial z^{l}}{\partial z^{l-1}})^T\delta^{l} = \delta^{l}*rot180(W^{l}) \odot \sigma^{‘}(z^{l-1})
\]
这里的式子其实和DNN的类似,区别在于对于含有卷积的式子求导时,卷积核被旋转了180度。即式子中的rot180(),翻转180度的意思是上下翻转一次,接着左右翻转一次。在DNN中这里只是矩阵的转置。那么为什么呢?由于这里都是张量,直接推演参数太多了。我们以一个简单的例子说明为啥这里求导后卷积核要翻转。
假设我们l?1层的输出\(a^{l?1}\)是一个3x3矩阵,第l层的卷积核\(W^l\)是一个2x2矩阵,采用1像素的步幅,则输出\(z^l\)是一个2x2的矩阵。我们简化\(b^l\)都是0,则有
\[a^{l-1}*W^l = z^{l}
\]
我们列出a,W,z的矩阵表达式如下:
\[\left( \begin{array}{ccc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{array} \right) * \left( \begin{array}{ccc} w_{11}&w_{12}\\ w_{21}&w_{22} \end{array} \right) = \left( \begin{array}{ccc} z_{11}&z_{12}\\ z_{21}&z_{22} \end{array} \right)
\]
利用卷积的定义,很容易得出:
\[z11=a11w11+a12w12+a21w21+a22w22z11=a11w11+a12w12+a21w21+a22w22\z12=a12w11+a13w12+a22w21+a23w22z12=a12w11+a13w12+a22w21+a23w22\z21=a21w11+a22w12+a31w21+a32w22z21=a21w11+a22w12+a31w21+a32w22\z22=a22w11+a23w12+a32w21+a33w22z22=a22w11+a23w12+a32w21+a33w22\\]
接着我们模拟反向求导:
\[\nabla a^{l-1} = \frac{\partial J(W,b)}{\partial a^{l-1}} = ( \frac{\partial z^{l}}{\partial a^{l-1}})^T\frac{\partial J(W,b)}{\partial z^{l}} =(\frac{\partial z^{l}}{\partial a^{l-1}})^T \delta^{l}
\]
从上式可以看出,对于\(a^{l-1}\)的梯度误差\(?a^{l-1}\),等于第l层的梯度误差乘以\(\cfrac{\partial z^{l}}{\partial a^{l-1}}\),而\(\cfrac{\partial z^{l}}{\partial a^{l-1}}\)对应上面的例子中相关联的\(w\)的值。假设我们的\(z\)矩阵对应的反向传播误差是\(δ11,δ12,δ21,δ22\)组成的2x2矩阵,则利用上面梯度的式子和4个等式,我们可以分别写出\(?a^{l-1}\)的9个标量的梯度。
比如对于\(a11\)的梯度,由于在4个等式中\(a11\)只和\(z11\)有乘积关系,从而我们有:
\[\nabla a_{11} = \delta_{11}w_{11}
\]
对于\(a12\)的梯度,由于在4个等式中\(a12\)和\(z12\),\(z11\)有乘积关系,从而我们有:
\[\nabla a_{12} = \delta_{11}w_{12} + \delta_{12}w_{11}
\]
同样的道理我们得到:
\[\nabla a_{13} = \delta_{12}w_{12}\\nabla a_{21} = \delta_{11}w_{21} + \delta_{21}w_{11}\\nabla a_{22} = \delta_{11}w_{22} + \delta_{12}w_{21} + \delta_{21}w_{12} + \delta_{22}w_{11}\\nabla a_{23} = \delta_{12}w_{22} + \delta_{22}w_{12}\\nabla a_{31} = \delta_{21}w_{21}\\nabla a_{32} = \delta_{21}w_{22} + \delta_{22}w_{21}\\nabla a_{33} = \delta_{22}w_{22}\\]
这上面9个式子其实可以用一个矩阵卷积的形式表示,即:
\[\left( \begin{array}{ccc} 0&0&0&0 \\ 0&\delta_{11}& \delta_{12}&0 \\ 0&\delta_{21}&\delta_{22}&0 \\ 0&0&0&0 \end{array} \right) * \left( \begin{array}{ccc} w_{22}&w_{21}\\ w_{12}&w_{11} \end{array} \right) = \left( \begin{array}{ccc} \nabla a_{11}&\nabla a_{12}&\nabla a_{13} \\ \nabla a_{21}&\nabla a_{22}&\nabla a_{23}\\ \nabla a_{31}&\nabla a_{32}&\nabla a_{33} \end{array} \right)
\]
为了符合梯度计算,我们在误差矩阵周围填充了一圈0,此时我们将卷积核翻转后和反向传播的梯度误差进行卷积,就得到了前一次的梯度误差。这个例子直观的介绍了为什么对含有卷积的式子反向传播时,卷积核要翻转180度的原因。
以上就是卷积层的误差反向传播过程。
DeepLearning C4中的公式:
\[dA += \sum _{h=0} ^{n_H} \sum_{w=0} ^{n_W} W_c \times dZ_{hw}
\]
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
这样写W不用转置:类似于反卷积的操作:
\[\left( \begin{array}{cc}\delta_{11}& \delta_{12} \\ \delta_{21}&\delta_{22}\\ \end{array} \right) *^{-1} \left( \begin{array}{cc} w_{11}&w_{12}\\ w_{21}&w_{22} \end{array} \right) = \left( \begin{array}{ccc} \nabla a_{11}&\nabla a_{12}&\nabla a_{13} \\ \nabla a_{21}&\nabla a_{22}&\nabla a_{23}\\ \nabla a_{31}&\nabla a_{32}&\nabla a_{33} \end{array} \right)
\]
5. 已知卷积层的\(\delta^l\),推导该层的W,b的梯度
好了,我们现在已经可以递推出每一层的梯度误差\(\delta^l\)了,对于全连接层,可以按DNN的反向传播算法求该层W,bW,b的梯度,而池化层并没有W,bW,b,也不用求W,bW,b的梯度。只有卷积层的W,bW,b需要求出。
注意到卷积层zz和W,bW,b的关系为:
\[z^l = a^{l-1}*W^l +b
\]
因此我们有:
\[\frac{\partial J(W,b)}{\partial W^{l}}=a^{l-1} *\delta^l
\]
注意到此时卷积核并没有反转,主要是此时是层内的求导,而不是反向传播到上一层的求导。具体过程我们可以分析一下。
和第4节一样的一个简化的例子,这里输入是矩阵,不是张量,那么对于第l层,某个个卷积核矩阵W的导数可以表示如下:
\[\frac{\partial J(W,b)}{\partial W_{pq}^{l}} = \sum\limits_i\sum\limits_j(\delta_{ij}^la_{i+p-1,j+q-1}^{l-1})
\]
假设我们输入aa是4x4的矩阵,卷积核WW是3x3的矩阵,输出zz是2x2的矩阵,那么反向传播的zz的梯度误差δδ也是2x2的矩阵。
那么根据上面的式子,我们有:
\[\frac{\partial J(W,b)}{\partial W_{11}^{l}} = a_{11}\delta_{11} + a_{12}\delta_{12} + a_{21}\delta_{21} + a_{22}\delta_{22}\\frac{\partial J(W,b)}{\partial W_{12}^{l}} = a_{12}\delta_{11} + a_{13}\delta_{12} + a_{22}\delta_{21} + a_{23}\delta_{22}\\frac{\partial J(W,b)}{\partial W_{13}^{l}} = a_{13}\delta_{11} + a_{14}\delta_{12} + a_{23}\delta_{21} + a_{24}\delta_{22}\\frac{\partial J(W,b)}{\partial W_{21}^{l}} = a_{21}\delta_{11} + a_{22}\delta_{12} + a_{31}\delta_{21} + a_{32}\delta_{22}
\]
最终我们可以一共得到9个式子。整理成矩阵形式后可得:
\[\frac{\partial J(W,b)}{\partial W^{l}} =\left( \begin{array}{ccc} a_{11}&a_{12}&a_{13}&a_{14} \\ a_{21}&a_{22}&a_{23}&a_{24} \\ a_{31}&a_{32}&a_{33}&a_{34} \\ a_{41}&a_{42}&a_{43}&a_{44} \end{array} \right) * \left( \begin{array}{ccc} \delta_{11}& \delta_{12} \\ \delta_{21}&\delta_{22} \end{array} \right)
\]
用dz做卷积刚好得到 W size 的矩阵:

从而可以清楚的看到这次我们为什么没有反转的原因。
DeepLearning C4中的公式:
\[dW_c += \sum _{h=0} ^{n_H} \sum_{w=0} ^ {n_W} a_{slice} \times dZ_{hw}
\]
哪个\(a^{l-1}\)的slice生成对应的\(z^{l}\)元素就和对应的\(dz^{l}\)元素相乘叠加到dW上
dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
求db:b一个filter对应一个 , 与该filter生成的Zc上的所有值相关
$$ db = \sum_h \sum_w dZ_{hw} $$
db[:,:,:,c] += dZ[i, h, w, c]
而对于b,则稍微有些特殊,因为 \(\delta^l\) 是高维张量,而 \(b\) 只是一个向量,不能像DNN那样直接和 \(\delta^l\) 相等。通常的做法是将 \(\delta^l\) 的各个子矩阵的项分别求和,得到一个误差向量,即为b的梯度:
\[\frac{\partial J(W,b)}{\partial b^{l}} = \sum\limits_{u,v}(\delta^l)_{u,v}
\]
6. CNN反向传播算法总结
现在我们总结下CNN的反向传播算法,以最基本的批量梯度下降法为例来描述反向传播算法。
输入:m个图片样本,CNN模型的层数L和所有隐藏层的类型,对于卷积层,要定义卷积核的大小K,卷积核子矩阵的维度F,填充大小P,步幅S。对于池化层,要定义池化区域大小k和池化标准(MAX或Average),对于全连接层,要定义全连接层的激活函数(输出层除外)和各层的神经元个数。梯度迭代参数迭代步长α,最大迭代次数MAX与停止迭代阈值?
输出:CNN模型各隐藏层与输出层的W,b
让我们对卷积神经网络的训练过程进行一个总结:
-
对神经网络进行初始化,定义好网络结构,设定好激活函数,对卷积层的卷积核W、偏置b进行随机初试化,对全连接层的权重矩阵W和偏置b进行随机初始化。
设置好训练的最大迭代次数,每个训练batch的大小,学习率 $ η$
-
从训练数据中取出一个batch的数据
-
从该batch数据中取出一个数据,包括输入x以及对应的正确标注y
-
将输入x送入神经网络的输入端,得到神经网络各层输出参数\(z^l\)和\(a^l\)
-
根据神经网络的输出和标注值y计算神经网络的损失函数
-
计算损失函数对输出层的delta误差\(\delta^L\)
-
利用相邻层之间delta误差的递推公式求得每一层的delta误差
如果是全连接层 \(dZl=\delta^{l} =(W^{l+1})^T\delta^{l+1}\odot\sigma‘(z^l)\,\)
如果是卷积层 \(\delta^{l} = \delta^{l+1}*rot180(W^{l+1}) \odot \sigma^{‘}(z^{l})\)
如果是池化层 \(\delta^{l} = upsample(\delta^{l+1}) \odot \sigma^{‘}(z^{l})\)
-
利用每一层的delta误差求出损失函数对该层参数的导数
如果是全连接层:\(dWl=\delta^l(a^{l-1})^T\\\,\\dbl=\delta^l\)
如果是卷积层:
\(\cfrac{\partial J(W,b)}{\partial W^{l}}=a^{l-1} *\delta^l\),\(\cfrac{\partial J(W,b)}{\partial b^{l}} = \sum\limits_{u,v}(\delta^l)_{u,v}\)
-
将求得的导数加到该batch数据求得的导数之和上(初始化为0),跳转到步骤3,直到该batch数据都训练完毕
-
利用一个batch数据求得的导数之和,根据梯度下降法对参数进行更新: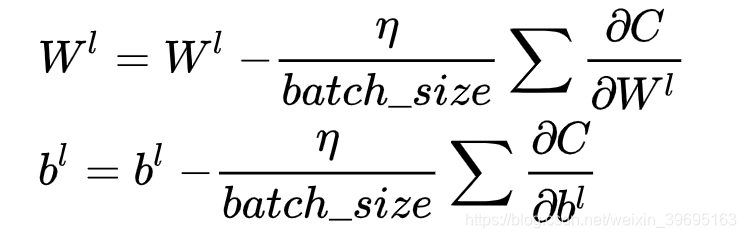
-
跳转到步骤2,直到达到指定的迭代次数
reference:
[1]刘建平Pinard:卷积神经网络(CNN)反向传播算法https://www.cnblogs.com/pinard/p/6494810.html
[2]卷积神经网络(CNN)反向传播算法推导https://zhuanlan.zhihu.com/p/61898234
CNN卷积神经网络的反向传播算法
原文:https://www.cnblogs.com/chenkaipku/p/14410595.html