1D Poisson's Equation - Finite Element

• 算法特征:
  ①. 选定基函数; ②. 作用测试函数; ③. 求解弱形式
• 算法推导:
  Part Ⅰ: 投影之引入
  本文拟采用$L_2$范数衡量函数距离. 在给定函数空间$X$中, 获取函数$f$在区间$[a, b]$的最优逼近, 即
  \begin{equation}
  \min_{g\ \in\ X}\quad \mathrm{dist}(f, g) = \left ( \int_a^b(f - g)^2 \mathrm{d}x \right )^{1 / 2} \quad\Rightarrow\quad \min_{g\ \in\ X}\quad \int_a^b(f - g)^2 \mathrm{d}x
  \label{eq_1}
  \end{equation}
  现令$g = g^\ast + g^\prime$, 则
  \begin{equation}
  \begin{split}
  \int_a^b (f - g)^2 \mathrm{d}x &= \int_a^b (f - g^\ast - g^\prime)^2 \mathrm{d}x \\
  &= \int_a^b (f - g^\ast)^2 - 2g^\prime (f - g^\ast) + g^{\prime 2}\mathrm{d}x
  \end{split}
  \label{eq_2}
  \end{equation}
  如果函数$g^\ast$为函数$f$在空间$X$的投影, 则
  \begin{equation}
  \int_a^b g^\prime (f - g^\ast) \mathrm{d}x = 0
  \label{eq_3}
  \end{equation}
  结合式$\eqref{eq_2}$, 有
  \begin{equation}
  \int_a^b (f - g)^2 \mathrm{d}x = \int_a^b (f - g^\ast)^2 \mathrm{d}x + \int_a^b g^{\prime 2}\mathrm{d}x
  \label{eq_4}
  \end{equation}
  由于$g$是任意的, $g^\ast$是$f$的投影, 则$g^\prime$是任意的, 结合式$\eqref{eq_1}$与式$\eqref{eq_4}$,
  \begin{equation}
  g^\ast = \mathop{\arg\min}_{g\ \in\ X}\ \mathrm{dist}(f, g)
  \label{eq_5}
  \end{equation}
  即函数$f$在给定函数空间$X$中的最优逼近即为它的投影. 由此也将式$\eqref{eq_1}$之优化问题等效为式$\eqref{eq_3}$之方程求解.
  Part Ⅱ: 投影之计算
  在给定函数空间$X$(假定为$n$维线性函数空间)中选择一组完备的基函数$\{ \phi_1, \phi_2, \cdots, \phi_n \}$, 则
  \begin{equation}
  g^\ast = \sum_{i=1}^n a_i\phi_i
  \label{eq_6}
  \end{equation}
  代入式$\eqref{eq_3}$, 有
  \begin{equation}
  \int_a^b g^\prime (f - \sum_{i=1}^n a_i\phi_i)\mathrm{d}x = 0
  \label{eq_7}
  \end{equation}
  由于$g^\prime$在投影空间中是任意的, 可取任意基函数作为测试函数, 上式转换如下,
  \begin{equation}
  \int_a^b \phi_j (f - \sum_{i=1}^n a_i\phi_i)\mathrm{d}x = \int_a^b \phi_j f \mathrm{d}x - \sum_{i=1}^n a_i\int_a^b\phi_j\phi_i\mathrm{d}x = 0, \quad \mathrm{where}\ j = 1, \cdots, n
  \label{eq_8}
  \end{equation}
  令,
  \begin{equation*}
  A = \begin{bmatrix}
  \int_a^b\phi_1\phi_1\mathrm{d}x & \cdots & \int_a^b\phi_1\phi_n\mathrm{d}x   \\
  \vdots & \ddots & \vdots   \\
  \int_a^b\phi_n\phi_1\mathrm{d}x & \cdots & \int_a^b\phi_n\phi_n\mathrm{d}x
  \end{bmatrix} \quad
  b = \begin{bmatrix}
  \int_a^b\phi_1 f\mathrm{d}x   \\
  \vdots   \\
  \int_a^b\phi_n f\mathrm{d}x
  \end{bmatrix} \quad
  \alpha = \begin{bmatrix}
  a_1   \\
  \vdots   \\
  a_n
  \end{bmatrix}
  \end{equation*}
  式$\eqref{eq_8}$转换如下,
  \begin{equation}
  A\alpha = b
  \label{eq_9}
  \end{equation}
  求解上式中$\alpha$, 即完成投影之计算.
  Part Ⅲ: 1维泊松方程求解
  给定如下1维泊松方程及其边界条件,
  \begin{equation}
  \frac{\partial^2 u}{\partial x^2} + f = 0, \quad u(a) = u(b) = 0
  \label{eq_10}
  \end{equation}
  作用任意测试函数$g(x)$, 并积分之,
  \begin{equation}
  \int_a^b g(\frac{\partial^2 u}{\partial x^2} + f)\mathrm{d}x = 0
  \label{eq_11}
  \end{equation}
  对上式$\eqref{eq_11}$分部积分, 引入弱形式,
  \begin{equation}
  g\frac{\partial u}{\partial x}\bigg|_a^b - \int_a^b\frac{\partial g}{\partial x}\cdot \frac{\partial u}{\partial x}\mathrm{d}x + \int_a^b gf\mathrm{d}x = 0
  \label{eq_12}
  \end{equation}
  本文拟选在分段线性空间中获取$u$的数值解. 分段线性空间常用基函数如下,
  \begin{equation}
  \phi_i(x) = \begin{cases}
  1, \quad \mathrm{where}\ x = x_i   \\
  0, \quad \mathrm{where}\ x \neq x_i
  \end{cases}
  \label{eq_13}
  \end{equation}
  其中, $x_i$表示网格节点. 本文将区间$[a, b]$剖为$n$份, 则$i = 0, 1, \cdots, n$, 且$x_0 = a$, $x_n = b$.
  根据基函数的特征, 令
  \begin{equation}
  u = \sum_{i=0}^n u_i\phi_i = u(a)\phi_0 + u(b)\phi_n + \sum_{i=1}^{n-1} u_i\phi_i = \sum_{i=1}^{n-1} u_i\phi_i
  \label{eq_14}
  \end{equation}
  取测试函数$g(x)$为基函数$\phi_1, \phi_2, \cdots, \phi_{n-1}$, 结合上式$\eqref{eq_14}$, 弱形式$\eqref{eq_12}$转换如下,
  \begin{equation}
  -\sum_{i=1}^{n-1}u_i\int_a^b\frac{\partial \phi_j}{\partial x}\cdot\frac{\partial \phi_i}{\partial x}\mathrm{d}x + \int_a^b\phi_j f\mathrm{d}x = 0, \quad\mathrm{where}\ j = 1, \cdots, n-1
  \label{eq_15}
  \end{equation}
  令,
  \begin{equation*}
  A = \begin{bmatrix}
  \int_a^b \frac{\partial\phi_1}{\partial x}\frac{\partial\phi_1}{\partial x}\mathrm{d}x & \cdots & \int_a^b\frac{\partial \phi_1}{\partial x}\frac{\partial \phi_{n-1}}{\partial x}\mathrm{d}x   \\
  \vdots & \ddots & \vdots   \\
  \int_a^b \frac{\partial\phi_{n-1}}{\partial x}\frac{\partial\phi_1}{\partial x}\mathrm{d}x & \cdots & \int_a^b\frac{\partial \phi_{n-1}}{\partial x}\frac{\partial \phi_{n-1}}{\partial x}\mathrm{d}x   \\
  \end{bmatrix}\quad
  b = \begin{bmatrix}
  \int_a^b \phi_1 f\mathrm{d}x   \\
  \vdots   \\
  \int_a^b \phi_{n-1} f\mathrm{d}x   \\
  \end{bmatrix}\quad
  \alpha = \begin{bmatrix}
  u_1   \\
  \vdots   \\
  u_{n-1}   \\
  \end{bmatrix}
  \end{equation*}
  式$\eqref{eq_15}$转换如下,
  \begin{equation}
  A\alpha = b
  \label{eq_16}
  \end{equation}
  求解上式中$\alpha$, 代入式$\eqref{eq_14}$即可获得泊松方程解$u$.
• 代码实现:
  Part Ⅰ:
  现以如下Poisson‘s equation为例进行算法实施,
  \begin{equation*}
  \frac{\partial^2 u}{\partial x^2} + \sin\pi x = 0, \quad u(0) = u(1) = 0
  \end{equation*}
  解析解如下,
  \begin{equation*}
  u = \frac{\sin\pi x}{\pi^2}
  \end{equation*}
  Part Ⅱ:
  利用finite element求解Poisson‘s equation, 实现如下:
  
  

    1 # Poisson‘s equation之实现 - 有限元法
    2 # 注意, 采用Gauss-Legendre Quadrature进行数值积分
    3 
    4 import numpy
    5 from matplotlib import pyplot as plt
    6 
    7 
    8 numpy.random.seed(0)
    9 
   10 
   11 # Gauss-Legendre Quadrature之实现
   12 def getGaussParams(num=6):
   13     if num == 1:
   14         X = numpy.array([0])
   15         A = numpy.array([2])
   16     elif num == 2:
   17         X = numpy.array([numpy.math.sqrt(1/3), -numpy.math.sqrt(1/3)])
   18         A = numpy.array([1, 1])
   19     elif num == 3:
   20         X = numpy.array([numpy.math.sqrt(3/5), -numpy.math.sqrt(3/5), 0])
   21         A = numpy.array([5/9, 5/9, 8/9])
   22     elif num == 6:
   23         X = numpy.array([0.238619186081526, -0.238619186081526, 0.661209386472165, -0.661209386472165, 0.932469514199394, -0.932469514199394])
   24         A = numpy.array([0.467913934574257, 0.467913934574257, 0.360761573028128, 0.360761573028128, 0.171324492415988, 0.171324492415988])
   25     elif num == 10:
   26         X = numpy.array([0.973906528517240, -0.973906528517240, 0.433395394129334, -0.433395394129334, 0.865063366688893, -0.865063366688893,  27             0.148874338981367, -0.148874338981367, 0.679409568299053, -0.679409568299053])
   28         A = numpy.array([0.066671344307672, 0.066671344307672, 0.269266719309847, 0.269266719309847, 0.149451349151147, 0.149451349151147,  29             0.295524224714896, 0.295524224714896, 0.219086362515885, 0.219086362515885])
   30     else:
   31         raise Exception(">>> Unsupported num = {} <<<".format(num))
   32     return X, A
   33 
   34 
   35 def getGaussQuadrature(func, a, b, X, A):
   36     ‘‘‘
   37     func: 原始被积函数
   38     a: 积分区间下边界
   39     b: 积分区间上边界
   40     X: 求积节点数组
   41     A: 求积系数数组
   42     ‘‘‘
   43     term1 = (b - a) / 2
   44     term2 = (a + b) / 2
   45     term3 = func(term1 * X + term2)
   46     term4 = numpy.sum(A * term3)
   47     val = term1 * term4
   48     return val
   49 
   50 
   51 class PoissonEq(object):
   52     
   53     def __init__(self, n, order=6):
   54         self.__n = n                                              # 子区间划分数
   55         self.__order = order                                      # Legendre多项式之阶数
   56         
   57         self.__X = self.__build_gridPoints(n)                     # 构造网格节点
   58         self.__XQuad, self.__AQuad = getGaussParams(order)        # 获取数值积分之求积节点、求积系数
   59         
   60         
   61     def get_solu(self):
   62         A = self.__build_A()
   63         b = self.__build_b()
   64         alpha = numpy.matmul(numpy.linalg.inv(A), b)
   65         
   66         U = numpy.zeros(self.__X.shape)
   67         U[1:-1] = alpha.flatten()
   68         
   69         return self.__X, U
   70         
   71         
   72     def __build_b(self):
   73         ‘‘‘
   74         构造列向量b
   75         ‘‘‘
   76         self.__xiMinusOne, self.__xi, self.__xiPlusOne = None, None, None
   77         
   78         b = numpy.zeros((self.__n-1, 1))
   79         for i in range(b.shape[0]):
   80             self.__xiMinusOne = self.__X[i]
   81             self.__xi = self.__X[i+1]
   82             self.__xiPlusOne = self.__X[i+2]
   83             quadValLeft = getGaussQuadrature(self.__funcLeft, self.__xiMinusOne, self.__xi, self.__XQuad, self.__AQuad)
   84             quadValRight = getGaussQuadrature(self.__funcRight, self.__xi, self.__xiPlusOne, self.__XQuad, self.__AQuad)
   85             b[i, 0] = quadValLeft + quadValRight
   86         return b
   87     
   88     
   89     def __funcLeft(self, x):
   90         val = (x - self.__xiMinusOne) / (self.__xi - self.__xiMinusOne) * numpy.sin(numpy.pi * x)
   91         return val
   92     
   93     
   94     def __funcRight(self, x):
   95         val = (self.__xiPlusOne - x) / (self.__xiPlusOne - self.__xi) * numpy.sin(numpy.pi * x)
   96         return val
   97         
   98         
   99     def __build_A(self):
  100         ‘‘‘
  101         构造矩阵A
  102         ‘‘‘
  103         dPhiLeft = 1 / (self.__X[1:-1] - self.__X[:-2])
  104         dPhiRight = -1 / (self.__X[2:] - self.__X[1:-1])
  105         interval = self.__X[1:] - self.__X[:-1]
  106         
  107         A = numpy.zeros((self.__n-1, self.__n-1))
  108         for i in range(A.shape[0]):
  109             for j in range(A.shape[1]):
  110                 if j == i-1:
  111                     A[i, j] = dPhiLeft[i] * dPhiRight[j] * interval[i]
  112                 elif j == i:
  113                     A[i, j] = dPhiLeft[i] * dPhiLeft[j] * interval[i] + dPhiRight[i] * dPhiRight[j] * interval[i+1]
  114                 elif j == i+1:
  115                     A[i, j] = dPhiRight[i] * dPhiLeft[j] * interval[i+1]
  116         return A
  117                     
  118         
  119     def __build_gridPoints(self, n):
  120         ‘‘‘
  121         随机初始化网格节点
  122         ‘‘‘
  123         xMin, xMax = 0, 1
  124         X = numpy.sort(numpy.random.uniform(xMin, xMax, n+1))
  125         X[0] = xMin
  126         X[-1] = xMax
  127         return X
  128         
  129         
  130 class PoissonPlot(object):
  131     
  132     @staticmethod
  133     def plot_fig(poissonObj):
  134         X, U = poissonObj.get_solu()
  135         
  136         xMin, xMax = numpy.min(X), numpy.max(X)
  137         X_ = numpy.linspace(xMin, xMax, 1000)
  138         U_ = numpy.sin(numpy.pi * X_) / numpy.pi ** 2
  139         
  140         fig = plt.figure(figsize=(6, 4))
  141         ax1 = plt.subplot()
  142         
  143         ax1.plot(X, U, marker=‘.‘, ls="--", label="numerical solution")
  144         ax1.plot(X_, U_, label="analytical solution")
  145         ax1.set(xlabel="$x$", ylabel="$u$")
  146         ax1.legend()
  147         fig.savefig("plot_fig.png", dpi=100)
  148         
  149         
  150         
  151 if __name__ == "__main__":
  152     n = 20
  153     order = 6
  154     poissonObj = PoissonEq(n, order)
  155     
  156     PoissonPlot.plot_fig(poissonObj)

  View Code
• 结果展示:
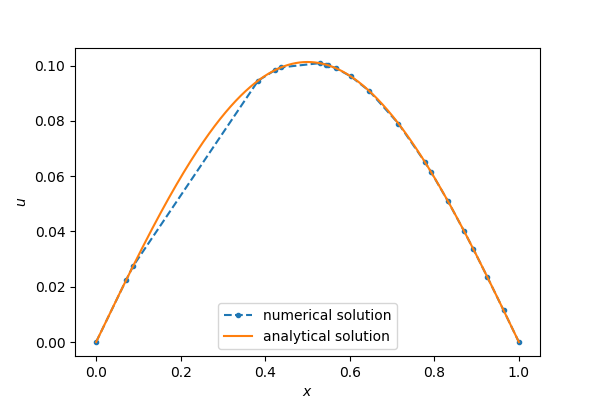  可以看到, 数值解与解析解是足够逼近的.
• 使用建议:
  ①. 微分方程转积分方程;
  ②. 分部积分求解弱形式.
• 参考文档:
  Numerical Methods for PDE 2016 by Professor Qiqi Wang & Jacob White from MIT

1D Poisson's Equation - Finite Element

原文：https://www.cnblogs.com/xxhbdk/p/14318749.html