奇异值分解
1. 特征值与特征向量
首先回顾特征值与特征向量定义
\[Ax=\lambda x
\]
\(A\)是一个\(n \times n\)矩阵,\(x\)是一个\(n\)维向量,则\(\lambda\)是矩阵\(A\)的一个特征值,而\(x\)是矩阵\(A\)的特征值\(\lambda\)对应的特征向量。
求出特征值和特征矩阵可以将矩阵\(A\)特征分解。如果求出矩阵\(A\)的\(n\)个特征值 \(\lambda_1 \le \lambda_2 \le ... \le \lambda_n\), 以及\(n\)个特征值所对应的特征向量\(\omega_1, \omega_2, ...., \omega_n\)
那么矩阵\(A\)就可以用下式的特征分解表示
\[A=W\Sigma W^{-1}
\]
其中\(W\)是这n个特征向量所张成的\(n \times n\)维矩阵,而\(\Sigma\)是这\(n\)个特征值为主对角线的\(n \times n\)矩阵。
一般会将\(W\)这\(n\)个特征向量标准化,即满足\(\parallel w_i \parallel_2 = 1\),或者\(w_i^Tw_i = 1\),此时的\(W\)的\(n\)个特征向量为标准正交基,满足\(W^TW=I\),即\(W^T = W^{-1}\),也就是说\(W\)为酉矩阵。
所以特征分解表达式可以写成
\[A=W\Sigma W^T
\]
进行特征值分解的矩阵必须为方阵。
2. 奇异值分解(SVD)
那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时需要使SVD。
2.1 SVD定义
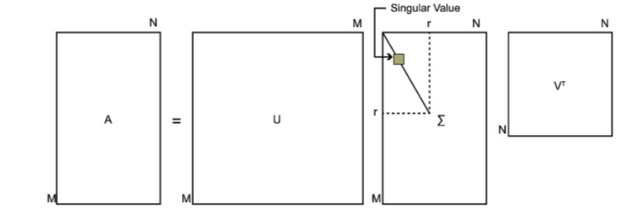
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵\(A\)是一个\(m×n\)的矩阵,那么我们定义矩阵\(A\)的SVD为:
\[A = U \Sigma V^T
\]
其中 \(U\)是一个 \(m \times m\)的矩阵, \(\Sigma\)是一个 \(m \times n\)的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值, \(V\)是一个 \(n \times n\)的矩阵。 \(U\)和 \(V\)都是酉矩阵,即满足
\[\begin{aligned}
U^TU = I \ V^TV = I
\end{aligned}
\]
下图表示SVD的定义
2.2 SVD的矩阵求解
如果我们将\(A^T\)和\(A\)做矩阵乘法,那么会得到n×n的一个方阵 \(A^TA\)。既然 \(A^TA\)是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
\[(A^TA)v_i = \lambda_iv_i
\]
这样我们就可以得到矩阵 \(A^TA\)的\(n\)个特征值和对应的\(n\)个特征向量\(v\)了。将 \(A^TA\)的所有特征向量张成一个\(n×n\)的矩阵\(V\),就是我们SVD公式里面的\(V\)矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将\(A\)和\(A^T\)做矩阵乘法,那么会得到\(m×m\)的一个方阵 \(AA^T\)。既然 \(AA^T\)是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
\[(AA^T)u_i = \lambda_iu_i
\]
这样我们就可以得到矩阵 \(A^TA\)的\(m\)个特征值和对应的\(m\)个特征向量\(u\)了。将 \(A^TA\)的所有特征向量张成一个\(m×m\)的矩阵\(U\),就是我们SVD公式里面的\(u\)矩阵了。一般我们将u中的每个特征向量叫做A的左奇异向量。
U和V我们都求出来了,现在就剩下奇异值矩阵Σ没有求出了.
由于Σ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值\(σ\)就可以了。
注意到:
\[\begin{aligned}
A &= U\Sigma V^T \ AV &= U \Sigma V^TV\ AV &= U\Sigma \ Av_i &= u_i\sigma_i \ \sigma_i&=\frac{Av_i}{u_i}
\end{aligned}
\]
这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵Σ
上面还有一个问题没有讲,就是我们说 \(A^TA\)的特征向量组成的就是我们SVD中的\(V\)矩阵,而\(A^TA\)的特征向量组成的就是我们SVD中的\(U\)矩阵,这有什么根据吗?这个其实很容易证明,我们以\(V\)矩阵的证明为例。
\[\begin{aligned}
A &= U\Sigma V^T \ A^T &= V\Sigma^T U^T \ A^TA &=V\Sigma^T U^TU\Sigma V^T \ &=V\Sigma^2V^T
\end{aligned}
\]
上式中\(\ \ U^TU = I \ \ \ \Sigma^T\Sigma = \Sigma^2\)。
可以看出\(A^TA\)的特征向量组成的的确就是我们SVD中的\(V\)矩阵。类似的方法可以得到\(AA^T\)的特征向量组成的就是我们SVD中的\(U\)矩阵
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
\[\sigma_i = \sqrt{\lambda_i}
\]
这样也就是说,我们可以不用\(σ_i=Av_i/u_i\)来计算奇异值,也可以通过求出\(A^TA\)的特征值取平方根来求奇异值。
2.3 SVD计算举例
用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为:
\[A =
\begin{pmatrix}
0 & 1 \1 & 1 \1 & 0 \\end{pmatrix}
\]
我们首先求出\(A^TA\)和\(AA^T\)
\[\begin{gathered}
A^TA = \begin{pmatrix}
0 & 1 & 1\1 & 1 & 0\\end{pmatrix}
\begin{pmatrix}
0 & 1 \1 & 1 \1 & 0 \\end{pmatrix}=
\begin{pmatrix}
2 & 1 \ 1 & 2
\end{pmatrix} \AA^T = \begin{pmatrix}
0 & 1 \1 & 1 \1 & 0 \\end{pmatrix}
\begin{pmatrix}
0 & 1 & 1\1 & 1 & 0\\end{pmatrix}=
\begin{pmatrix}
1 & 1 & 0\1 & 2 & 1\0 & 1 & 1\\end{pmatrix}
\end{gathered}
\]
进而求出\(A^TA\)的特征值和特征向量:
\[\lambda_1=3;v_1=\begin{pmatrix}
\frac{1}{\sqrt{2}}\ \ \frac{1}{\sqrt{2}}\\end{pmatrix};
\lambda_2=1;v_2=\begin{pmatrix}
-\frac{1}{\sqrt{2}}\ \ \frac{1}{\sqrt{2}}\\end{pmatrix};
\]
接着求\(AA^T\)的特征值和特征向量
\[\lambda_1=3;u_1=\begin{pmatrix}
\frac{1}{\sqrt{6}}\ \ \frac{2}{\sqrt{6}}\ \ \frac{1}{\sqrt{6}}\\end{pmatrix};
\lambda_2=1;u_2=\begin{pmatrix}
-\frac{1}{\sqrt{2}}\ \ 0\ \ -\frac{1}{\sqrt{2}}\\end{pmatrix};
\lambda_3=0;u_3=\begin{pmatrix}
\frac{1}{\sqrt{3}}\ \ -\frac{1}{\sqrt{3}}\ \ \frac{1}{\sqrt{3}}\\end{pmatrix};
\]
利用\(Av_i = \sigma_iu_i,i = 1,2\)求奇异值
\[\begin{gathered}
\begin{pmatrix}
0 & 1\ 1 & 1\ 1 & 0\ \end{pmatrix}
\begin{pmatrix}
\frac{1}{\sqrt{2}}\\ \ \frac{1}{\sqrt{2}}\ \end{pmatrix}=
\sigma_1
\begin{pmatrix}
\frac{1}{\sqrt{6}}\ \ \frac{2}{\sqrt{6}}\ \ \frac{1}{\sqrt{6}}\ \end{pmatrix}
\ \sigma_1 = \sqrt{3}
\ \begin{pmatrix}
0 & 1\ 1 & 1\ 1 & 0\ \end{pmatrix}
\begin{pmatrix}
- \frac{1}{\sqrt{2}}\\ \ \frac{1}{\sqrt{2}}\ \end{pmatrix}=
\sigma_2
\begin{pmatrix}
\frac{1}{\sqrt{2}}\ \ 0\ \ - \frac{1}{\sqrt{2}}\ \end{pmatrix}
\ \sigma_2 = 1
\end{gathered}
\]
也可以用\(\sigma_i = \sqrt{\lambda_i}\)直接求出奇异值为\(\sqrt{3}\)和\(1\)
最终得到A的奇异值分解为:
\[\begin{gathered}
A = U\Sigma V^T =
\begin{pmatrix}
1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3}\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\ 1/\sqrt{6} & -1/\sqrt{2}& 1/\sqrt{3}
\end{pmatrix}
\begin{pmatrix}
\sqrt{3} & 0\ 0 & 1\ 0 & 0
\end{pmatrix}
\begin{pmatrix}
1/\sqrt{2} & 1/\sqrt{2} \ -1/\sqrt{2} & 1/\sqrt{2} \ \end{pmatrix}
\end{gathered}
\]
2.4 SVD的一些性质
对于奇异值,它跟我们特征分解中的特征值类似, 在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。 也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说:
\[A_{m \times n} = U_{m \times m}\Sigma_{m \times n}V^T_{n \times n} \approx U_{m\times k}\Sigma_{k\times k}V^T_{k \times n}
\]
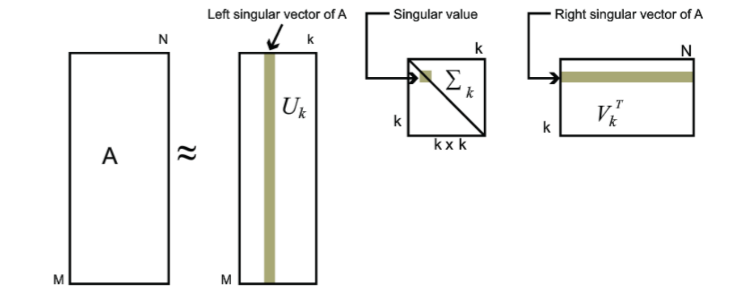
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。也可以用于推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI)。
2.6 小结
SVD作为一个很基本的算法,在很多机器学习算法中都有它的身影,特别是在现在的大数据时代,由于SVD可以实现并行化,因此更是大展身手。SVD的原理不难,只要有基本的线性代数知识就可以理解,实现也很简单因此值得仔细的研究。当然,SVD的缺点是分解出的矩阵解释性往往不强,有点黑盒子的味道,不过这不影响它的使用。
奇异值分解(SVD)
原文:https://www.cnblogs.com/jazzisfuture/p/14298437.html

