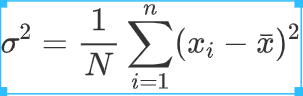【导读】今天我们继续以《数据挖掘概念与技术》(机械工业出版社,作者:Jiawei Han;Micheline Kamber;翻译:范明 / 孟小峰)一书为基础,配合Python代码给大家介绍数据属性、度量和基本统计描述图形。今天我们所涉及的内容依然非常基础,但却是后续不断会用到的一些概念和知识。笔者也将书中内容提炼成了层次更加清晰的思维导图, 并在jupyter notebook 中使用python书写了对应代码。你可以在我们的公众号"数据臭皮匠" 中回复"第二章xmind", 获取xmind格式的思维导图。回复"第二章代码",获取本文的jupyter代码
1、数据属性
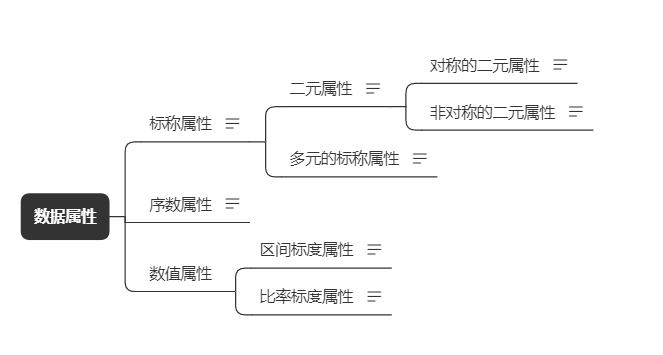
书中称数据属性。分为标称属性、序数属性、数值属性。尽管每个出处的叫法可能不一样,但其实就是我们很熟悉的数据分类的概念,下面大家可以感受下
类别型属性,不同类别间无法比较顺序, 如:职业类别, 颜色类别等
只有两个类别, 0表示属性不出现, 1表示出现 如,是否抽烟等
两种状态有相同的价值,携带相同的权重,如性别的男女属于对称的二元属性(一般 标识性别时男为1,女为0)
两种状态有着不一样的权重, 如艾滋病病毒化验结果,1 为阳性,0 为阴性,通常使用1表示重要的状态(HIV阳性), 另一个用0表示(HIV阴性)
可以排先后顺序, 单元素之间的差值无意义 如, 大中小, 很满意, 满意, 中性,不满意等
先后顺序, 差值都有意义, 但倍数无意义的属性, 如温度,可以说10度比5度高5度, 但无法说10度是5度的2倍, 因为0度不是表示没有温度。
具有固定零点的数值属性,这时候,先后排序,差值,倍数都是有意义的。如重量, 速度等(速度4m/s 是2m/s 的两倍
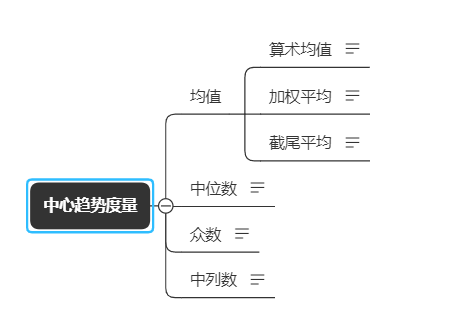
2、数值的中心趋势度量
令x1,x2... xn 为某一属性的n个观测值, 其均值为:
对于i = 1,2,.... n , 每个值xi 可以与一个权重wi 相关联,这时可以计算加权平均数:
(w1x1+w2x2+...+wnxn)/(w1+w2+...+wn)
截尾均值为丢弃高低极端值后的均值, 如公司的平均工资可能被几个高收入的经理拉高, 截尾均值能够抵消少数异常值的影响, 如计算平均工资时, 可以在计算均值之前先去掉前后2%(比例自己定义,但应避免截去太大比例, 因为会丢失太多信息)
先将N个数值按顺序排列, 中间的那个值就是中位数, 如果N为奇数,中位数为该有序集的中间值, 如果N为偶数, 一般取中间两个值的均值,中位数可以避免极端值对均值的影响, 一般收入中位数比收入均值更能代表总体收入水平
数据集的众数是指出现最频繁的值, 可以对定性和定量属性确定众数
中列数是数据最大值和最小值的均值, 即(max() + min())/2
3、数据的分散程度度量
设x1,x2...xn 为一个集合, 该集合的极差为最大值与最小值之差
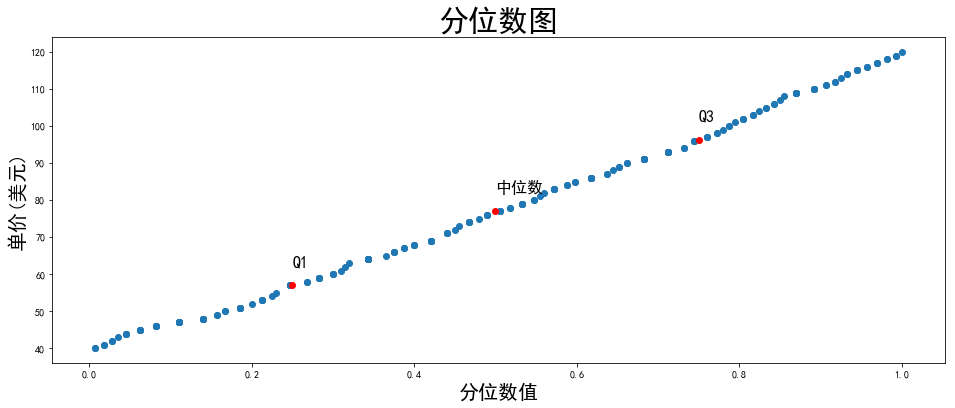
有三个点,将数据划分成相同大小的4个数据集合, 所以第一个四分位数Q1为第25%处,第二个百分位数Q2为50%处, 第三个分位数Q3为第75%处
Q3-Q1 即, 第三个四分位数与第一个四分位数的差值
由min, Q1,median, Q3,max 组成
即, 最小值, 四分位数Q1, 中位数,四分位数Q3和最大值组成
盒的端点在四分位上(Q1,Q3) , 中位数用盒内的线标记, 盒外的两条胡须延伸到最大值和最小值, 如果最大值比Q3大1.5倍的IQR(Q3-Q1) , 胡须延伸至1.5被IQR处, 最小值小于Q1 的1.5倍IQR, 向下的胡须延伸至1.5被IQR处, 超过胡须的点,单独的绘出(一般被认为离群点)
标准差是方差开根号的结果, 两者都可以指出数据分布的离散程度, 低标准差意味着数据更靠近均值, 高标准差意味着数据散布在较大的值域中。当数据集中数值完全一样时, 标准差为0, 否则标准差大于0 ,重要的是, 可以证明至少(1-1/k^2) * 100% 的观测值不超过k个标准差。
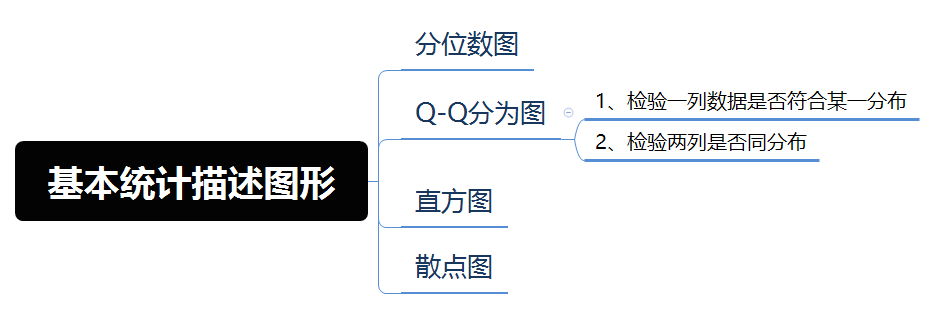
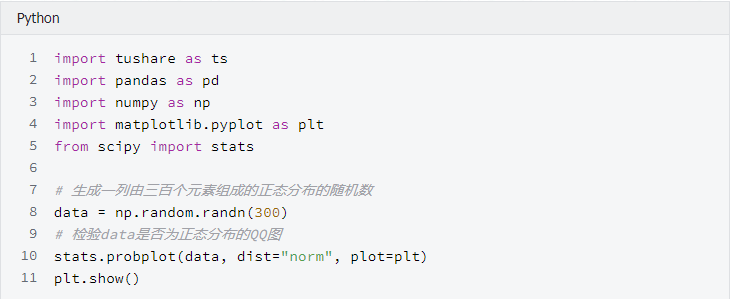
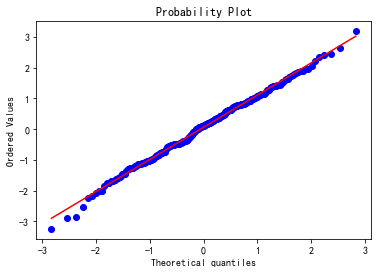
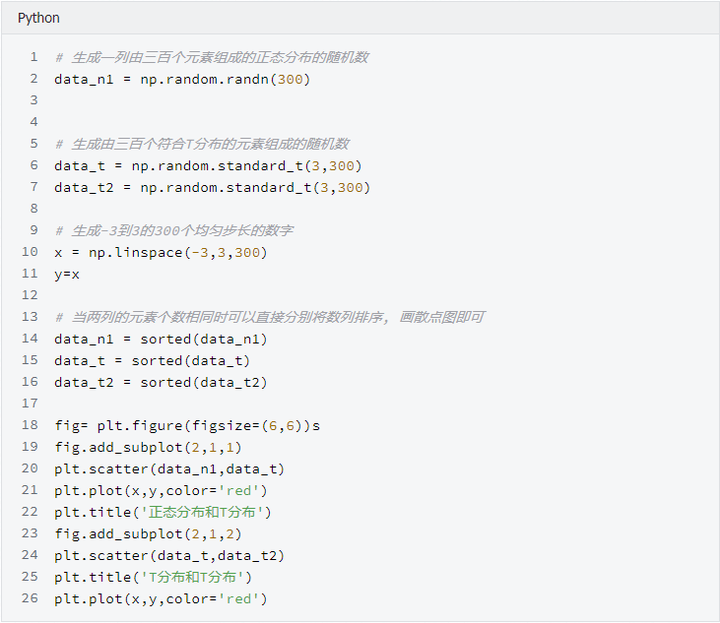
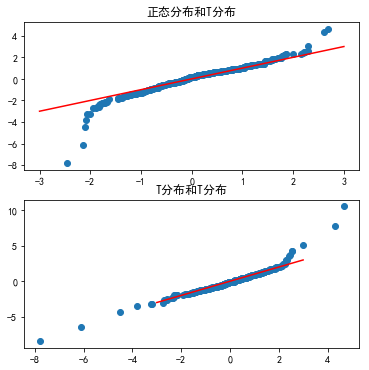
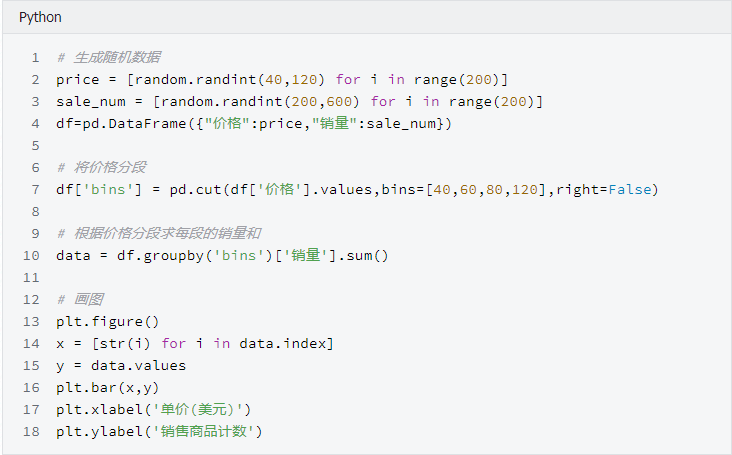
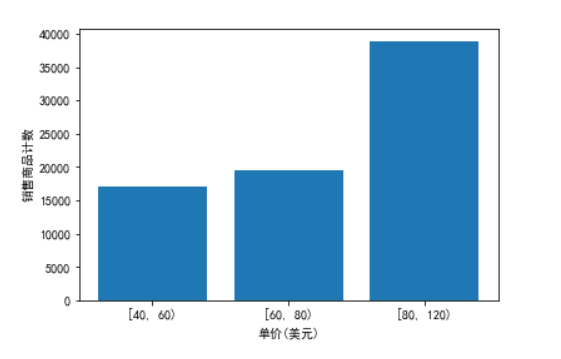
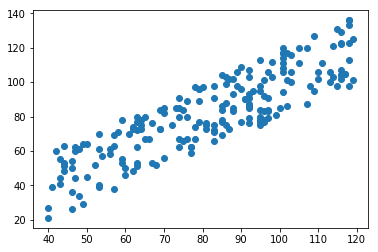
4、基本统计描述图形
数据挖掘概念与技术-第2章
原文:https://www.cnblogs.com/shujuchoupijiang/p/14295878.html