伪随机

1.

• \(\sum_{i=1}^6{p_i} = 1\)，每次计算完\(p_i\)以后需要归一化。
• \(n\)：抽了多少次奖
• times：是关于抽了多少次奖的函数，例如：\(0.02 - 0.1^n\)
• \(count_i\)：是关于第i个奖中了多少次的函数
• \(a_i\)是权重，且\(\sum{a_i} = 1\)初始：比如可以设置\(\alpha_2 = (n-3)^2 / 9, \alpha_1=1 - (n-3)^2/9\)。
• 当抽奖次数趋近于无穷时候，a1 -> 0，a2 -> 1，n趋近于给的图片上写好的的概率

当 \(0 <n <3\)，\(a_1\)增大，\(a_2\)减小，\(count_i\)可以设置为比如\(0.1^{中奖次数}, 0.5^{中奖次数}\)，看你想要多大的概率，然后\(n>3\)时，可以把\(a_1\)，\(a_2\)换成别的函数，例如：设置\(a_2\)等于下图所示sigmoid函数：

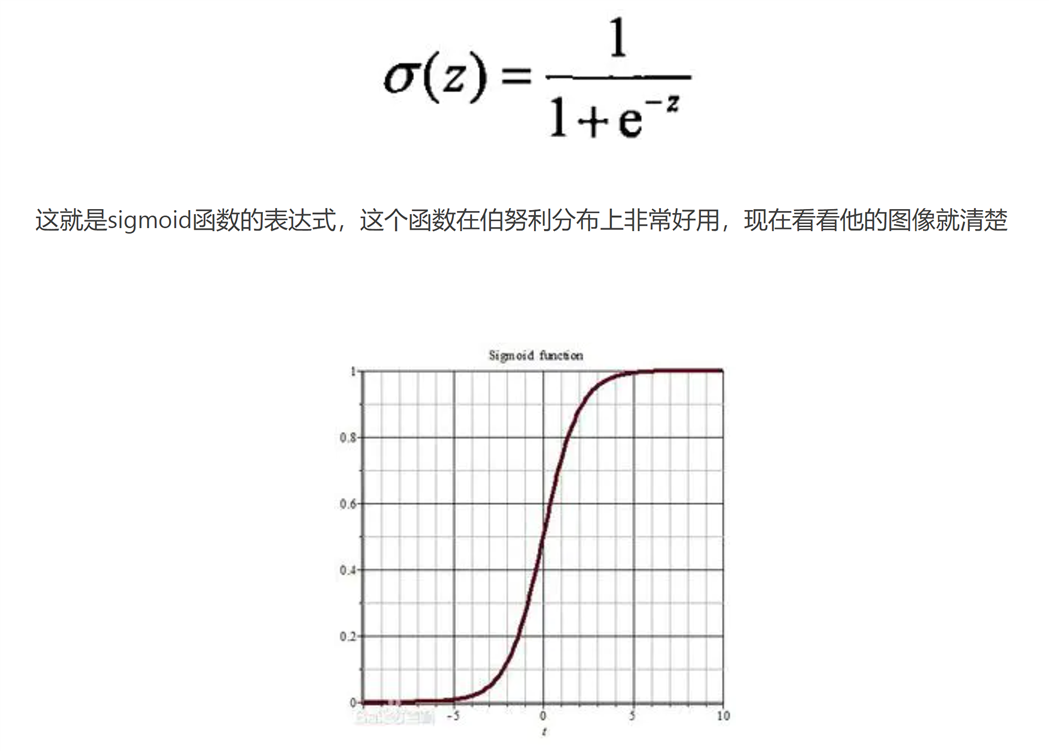
这样\(n >= 4\)的时候，基本上pi的概率就只跟后一项\(a_2*times\)相关，因为\(a_1\) -> 0, \(a_2\) -> 1

伪随机

原文：https://www.cnblogs.com/lsc2019/p/14173992.html