#include <iostream>
#include <cstdio>
using namespace std;
#define N 10 //代表生成0-9的子集
void print_subset(int n, int* A, int cur);
void print_subset(int n, int* A, int cur) { //代表增量构造法的函数,代表一次取出一个元素到集合中
int i = 0;
for (i = 0; i < cur; i++) { //代表输出集合
printf("%d ", A[i]);
}
printf("\n"); //输出集合后,要输出一个回车进行分隔(因此,当cur等于0时这里输出的是空集)
int s = cur ? A[cur - 1] + 1 : 0; //s代表确定当前元素的最小可能值(例如A中已经有了一个元素0,那么下次递归时cur就是1,那么当前元素的最小可能值就是A[cur-1]+1(因为A之中的元素编号都是从小到大排列的,这是定序的技巧(避免同一个集合枚举两次,例如:集合{1,2}输出时只能为{1,2}而不能为{2,1})
for (i = s; i < n; i++) { //i代表从最小可能值开始一直遍历到n-1,作为取出的集合元素
A[cur] = i; //将元素添加(取出)到集合A中(cur代表插入集合的位置)
print_subset(n, A, cur + 1); //进行递归(并将插入集合的位置+1)
}
}
int main() {
int A[10]; //代表进行生成的集合A
print_subset(N, A, 0);
}
#include <iostream>
#include <cstdio>
using namespace std;
#define N 10
void print_subset(int n, int* B, int cur); //代表构造位向量法的函数
void print_subset(int n, int* B, int cur) {
int i;
if (cur == n) { //当cur等于n时,代表一个集合已经构造完成
for (i = 0; i < cur; i++) { //代表输出集合
if (B[i]) { //如果B[i]为1代表在集合中存在元素i,否则就不存在元素i
printf("%d ", i); //输出元素i
}
}
printf("\n"); //输出回车以分隔集合
return; //输出完集合后,我们要进行返回(回溯)以便于输出下一个集合
}
B[cur] = 1; //代表选择当前元素(cur)添加到集合中
print_subset(n, B, cur + 1); //进行递归以便于选择下一个元素
B[cur] = 0; //代表不选择当前元素(cur)添加到集合中
print_subset(n, B, cur + 1); //进行递归以便于选择下一个元素
}
int main() {
int B[10]; //代表标记10个元素是否在集合当中的数组
print_subset(N, B, 0);
}
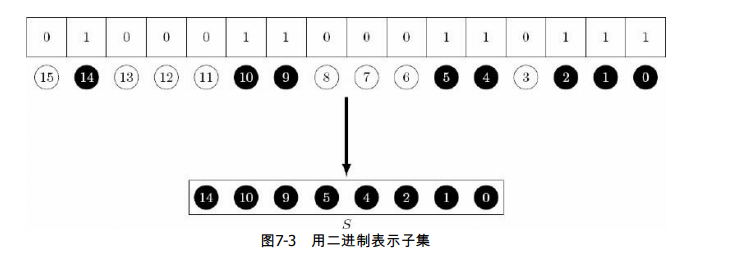

#include <iostream>
#include <cstdio>
using namespace std;
#define N 10
void print_subset(int n, int s); //代表构造二进制法的函数
void print_subset(int n, int s) { //代表构造二进制法并输出集合的函数
int i;
for (i = 0; i < n; i++) {
if (s & (1 << i)) {
printf("%d ", i);
}
}
printf("\n");
}
int main() {
int i;
for (i = 0; i < (1 << N); i++) { //代表遍历子集,其中(1<<N的意思为:对于有n个元素的集合,它的子集为2的n次方个)。那么,i就代表遍历的子集。
print_subset(N, i);
}
}
for (i = 0; i < n; i++) {
if (s & (1 << i)) {
printf("%d ", i);
}
}
原文:https://www.cnblogs.com/gao79135/p/14128453.html