因为各种原因鸽了一个月的博客。今天就把三种最短路都简单归纳一下记录一下。
首先介绍最短路的背景
#include<bits/stdc++.h> using namespace std; const int inf = 0x3f3f3f3f; const int maxn = 100; int map1[maxn][maxn]; int u,v,w; int main(){ int n,m,i,j,k; memset(map1,inf,sizeof(map1)); for(i = 1;i<=n;i++){ map1[i][i] = 0; } while(m--){ scanf("%d %d %d",&u,&v,&w); map1[u][v] = map1[v][u] = w; } for(k = 1;k<=n;k++){ for(i = 1;i<=n;i++){ for(k = 1;k<=n;k++){ if(map1[i][j]>map1[i][k]+map1[k][j]){ map1[i][j]>map1[i][k]+map1[k][j]; } } } } printf("%d\n",map1[1][n]); }
这里选择了使用邻接矩阵存图,原因是Floyd算法复杂度较高,一般用于解决规模较小的问题,所以不需要更高效率的存储工具,邻接矩阵可以很好的完成这个任务。
2.dijstra算法
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T,初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,OK,此时完成一个顶点,
然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
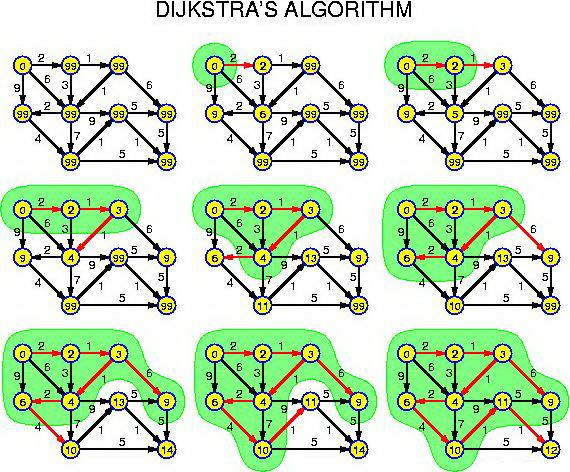
算法的思路也很清晰,我们先尝试用邻接矩阵来实现这个算法
#include<bits/stdc++.h> using namespace std; const int inf = 0x3f3f3f3f; const int maxn = 1000; int map1[maxn][maxn],dis[maxn]; bool vis[maxn]={false}; int u,v,w,n; void Dijkstra(int start) { vis[start]=true; for(int i=0;i<n;i++) dis[i]=map1[start][i]; dis[start]=0; for(int i=0;i<n;i++)//进行n次操作,i无实际意义 { int min1=inf;//最小值记录 int now=-1;//当前最短的点 for(int j=0;j<n;j++)//找到当前最短的dis[j] { if(!vis[j]&&dis[j]<min1) { min1=dis[j]; now=j; } } if(now==-1) return ; vis[now]=true; for(int j=0;j<n;j++) { if(!vis[j]&&map1[now][j]) { if(dis[j]>map1[now][j]+dis[now]) dis[j]=map1[now][j]+dis[now]; } } } } int main() { int m,s; cin>>n>>m>>s;//n个点,m条变,从s开始 for(int i=0;i<maxn;i++) for(int j=0;j<maxn;j++) map1[i][j]=inf; for(int i=0;i<m;i++) { cin>>u>>v>>w; map1[u][v]=w; } Dijkstra(s);//从s开始 for(int i=0;i<n;i++) { cout<<dis[i]<<endl; } return 0; }
可以发现这个算法的复杂度是O(n2)的虽然已经很优秀了,但是在面对一些更复杂问题的时候,这个复杂度还不够理想,于是我们想优化这个算法首先可以从空间上优化,我们可以用vector模拟链表存储从每个点出发的所有边的终点和权值。然后用优先队列维护每次选中的最短边。用vis或if (d[v] < p.first) continue;来防止多次重复,按bfs的思想结合优先队列,可以让这个算法的复杂度降低到O(nlogn)基本可以满足所有问题,就算求多源最短路,我们只用跑n次就能做到比Floyd优秀。
#include<bits/stdc++.h> using namespace std; int s, t, n, m, q; const int MAXV = 100005; struct edge { int to, cost; }; typedef pair<int, int> P; //first是最短距离,second是顶点的编号 int V;//顶点个数 vector<edge> G[MAXV]; int d[MAXV]; int vis[MAXV]; void Dijkstra(int s) { priority_queue<P, vector<P>, greater<P> > que; for(int i = 1; i <= 100000; i++) d[i] = 2000000000; d[s] = 0; que.push(P(0, s)); //把起点推入队列 while(!que.empty()) { P p = que.top(); que.pop(); int v = p.second; //顶点的编号 /*if(vis[v])continue;//防止节点的重复扩展 vis[v]=1;*/ if (d[v] < p.first) continue; for(int i = 0; i < G[v].size(); i++) { edge e = G[v][i]; if (d[e.to] > d[v] + e.cost) { d[e.to] = d[v] + e.cost; que.push(P(d[e.to], e.to)); } } } } int main() { cin >> n >> m >> s; for(int i = 1; i <= n; i++) G[i].clear(); edge temp; for(int i = 1; i <= m; i++) { cin >> q >> temp.to >> temp.cost; G[q].push_back(temp); } Dijkstra(s); for(int i = 1; i <= n; i++) { if(d[i] != 2000000000)cout << d[i] << " "; else cout << 2147483647 << " "; } cout << endl; return 0; }
如果追求更优秀的效率,那么用链式前向星存图大约可以优化五分之一左右的常数,代码也附在楼下
#include<bits/stdc++.h> const int MaxN = 100010, MaxM = 500010; struct edge { int to, dis, next; }; edge e[MaxM]; int head[MaxN], dis[MaxN], cnt; bool vis[MaxN]; int n, m, s; inline void add_edge( int u, int v, int d ) { cnt++; e[cnt].dis = d; e[cnt].to = v; e[cnt].next = head[u]; head[u] = cnt; } struct node { int dis; int pos; bool operator <( const node &x )const { return x.dis < dis; } }; std::priority_queue<node> q; inline void dijkstra() { dis[s] = 0; q.push( ( node ) { 0, s } ); while( !q.empty() ) { node tmp = q.top(); q.pop(); int x = tmp.pos, d = tmp.dis; if( vis[x] ) continue; vis[x] = 1; for( int i = head[x]; i; i = e[i].next ) { int y = e[i].to; if( dis[y] > dis[x] + e[i].dis ) { dis[y] = dis[x] + e[i].dis; if( !vis[y] ) { q.push( ( node ) { dis[y], y } ); } } } } } int main() { scanf( "%d%d%d", &n, &m, &s ); for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff; for( register int i = 0; i < m; ++i ) { register int u, v, d; scanf( "%d%d%d", &u, &v, &d ); add_edge( u, v, d ); } dijkstra(); for( int i = 1; i <= n; i++ ) printf( "%d ", dis[i] ); return 0; }
3.spfa算法
算法思路
我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
很多时候我们并不需要那么多无用的松弛操作。这时候就不再看边了,而是看点,如果dis[i]刷新了,那么说明这个i点可以为我们接下来的松弛提供帮助,我们应该将它记录起来。
那么我们用队列来维护“可能会引起松弛操作的点”,就可以只访问必要的边了,从而省去没必要的操作。
还要注意一点,这个队列里的元素是可以重复入队的,因为一个点的最短路径可以不断更新。另外,当一个点已经在队列里的时候,我们是不用将它入队的,因为我们记录这个点的目的是等会要使用它,所以我们记的是它的编号。 这里一定要和Dij的堆优化分清楚,Dij堆优化的队列里面存的是路径长度,我们这里不需要,所以就算这个点的最短路径中间可能会变,但是不影响我们的结果,我们只需要记住这个点可能可以作为松弛的中转点,也就是我们可以用它进行松弛,就够了。
但是这个算法的问题在于,面对菊花图的数据,它的复杂度会降低到O(n2),所以如果没有负边权的情况下,最好不要使用
代码如下
#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; struct node { int v, w, next; }edge[5000005]; int n, tot; int head[1000005], dis[1000005]; bool vis[1000005]; void add_edge(int u,int v,int w) { tot++; edge[tot].v = v; edge[tot].w = w; edge[tot].next = head[u]; head[u]=tot; } void spfa(int x) { queue <int> q; for(int i=1;i<=n;i++) { dis[i] = INF; vis[i] = 0; } dis[x] = 0; vis[x] = 1; q.push(x); while(!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for(int i=head[u]; i; i=edge[i].next) { int v = edge[i].v; if(dis[v] > dis[u]+edge[i].w) { dis[v] = dis[u]+edge[i].w; if(!vis[v]) { vis[v] = 1; q.push(v); } } } } } int main() { int m; ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin >> n >> m; tot = 0; while(m--) { int u, v; cin >> u >> v; add_edge(u, v, 1); add_edge(v, u, 1); } spfa(1); for(int i=1; i<=n; i++) cout << i << " " << dis[i] << endl; return 0; }
总结,实际上关于什么时候选取那个最短路路算法,很容易就能看出来,如果数据规模小且是多源最短路,那么无论如何都可以选取Floyd算法。如果有负边权而且数据范围较大,用spfa算法,其他情况都可以用dijkstar算法解决,不管是多源最短路还是单源最短路。他都是稳定且优秀的最佳算法。
原文:https://www.cnblogs.com/tscjj/p/14100659.html