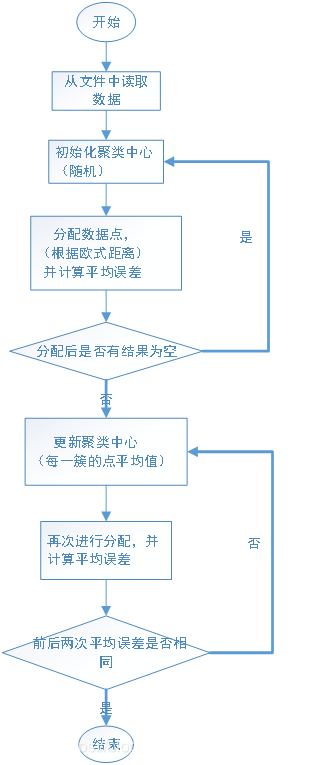
一、k-means算法思想:
第一步,从文件中读取数据,点用元组表示,点集用列表表示。
第二步,初始化聚类中心。首先获取数据的长度,然后在range(0,length)这个区间上随机产生k个不同的值,以此为下标提取出数据点,将它们作为聚类初始中心,产生列表center。
第三步,分配数据点。将数据点分配到距离(欧式距离)最短的聚类中心中,产生列表assigment,并计算平均误差。
第四步,如果首次分配后有结果为空,则重新初始化聚类中心。
第五步,更新聚类中心,(计算每一簇中所有点的平均值),然后再次进行分配,并计算平均误差。
第六步,比较前后两次的平均误差是否相等,若不相等则进行循环,否则终止循环,进入下一步
最少进行两次聚类,对比误差,输出较小误差时的结果,避免平均误差过大。
二、流程图:
三、 结果输出:

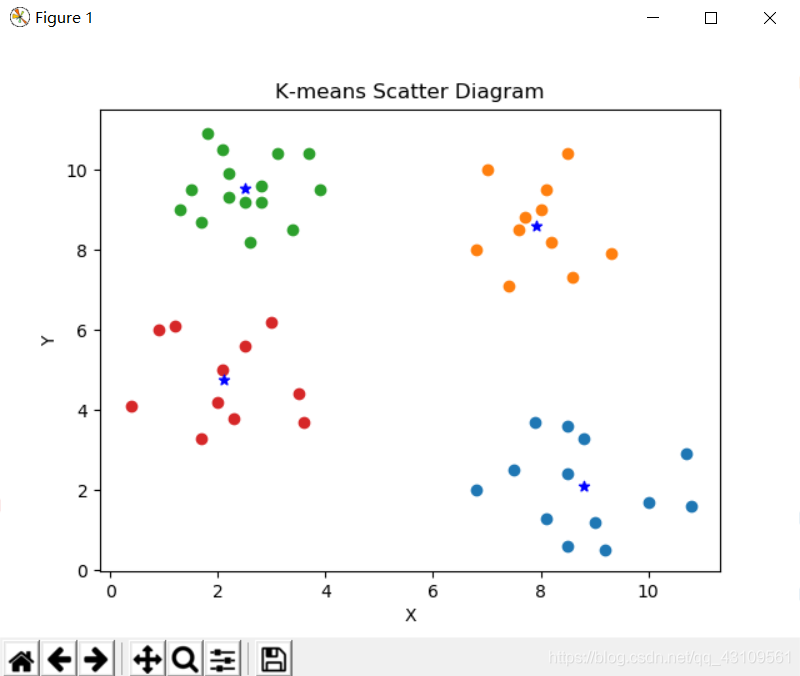
四、散点图:
五、python实现代码:
1 import random 2 from math import * 3 import matplotlib.pyplot as plt 4 5 #从文件种读取数据 6 def read_data(): 7 data_points = [] 8 with open(‘data.txt‘,‘r‘) as fp: 9 for line in fp: 10 if line ==‘\n‘: 11 continue 12 data_points.append(tuple(map(float,line.split(‘ ‘))))#去掉空格,并将data中数据的类型转为tuple 13 fp.close() 14 return data_points 15 16 #初始化聚类中心 17 def begin_cluster_center(data_points,k): 18 center=[] 19 length=len(data_points)#长度 20 rand_data = random.sample(range(0,length), k)#生成k个不同随机数 21 for i in range(k):#得出k个聚类中心(随机选出) 22 center.append(data_points[rand_data[i]]) 23 return center 24 25 #计算最短距离(欧式距离) 26 def distance(a,b): 27 length=len(a) 28 sum = 0 29 for i in range(length): 30 sq = (a[i] - b[i]) ** 2 31 sum += sq 32 return sqrt(sum) 33 #分配样本 34 # 按照最短距离将所有样本分配到k个聚类中心中的某一个 35 def assign_points(data_points,center,k): 36 assignment=[] 37 for i in range(k): 38 assignment.append([]) 39 for point in data_points: 40 min = 10000000 41 flag = -1 42 for i in range(k): 43 value=distance(point,center[i])#计算每个点到聚类中心的距离 44 if value<min: 45 min=value#记录距离的最小值 46 flag=i #记录此时聚类中心的下标 47 assignment[flag].append(point) 48 return assignment 49 50 #更新聚类中心,计算每一簇中所有点的平均值 51 def update_cluster_center(center,assignment,k): 52 for i in range(k):#assignment中的每一簇 53 x=0 54 y=0 55 length=len(assignment[i])#每一簇的长度 56 if length!=0: 57 for j in range(length): # 每一簇中的每个点 58 x += assignment[i][j][0] # 横坐标之和 59 y += assignment[i][j][1] # 纵坐标之和 60 center[i] = (x / length, y / length) 61 return center 62 63 #计算平方误差 64 def getE(assignment,center): 65 sum_E=0 66 for i in range(len(assignment)): 67 for j in range(len(assignment[i])): 68 sum_E+=distance(assignment[i][j],center[i]) 69 return sum_E 70 71 #计算各个聚类中心的新向量,更新距离,即每一类中每一维均值向量。 72 # 然后再进行分配,比较前后两个聚类中心向量是否相等,若不相等则进行循环, 73 # 否则终止循环,进入下一步。 74 def k_means(data_points,k): 75 # 由于初始聚类中心是随机选择的,十分影响聚类的结果,聚类可能会出现有较大误差的现象 76 # 因此如果由初始聚类中心第一次分配后有结果为空,重新选择初始聚类中心,重新再聚一遍,直到符合要求 77 while 1: 78 # 产生初始聚类中心 79 begin_center = begin_cluster_center(data_points, k) 80 # 第一次分配样本 81 assignment = assign_points(data_points, begin_center, k) 82 for i in range(k): 83 if len(assignment[i]) == 0:#第一次分配之后有结果为空,说明聚类中心没选好,重新产生初始聚类中心 84 continue 85 break 86 #第一次的平方误差 87 begin_sum_E=getE(assignment,begin_center) 88 # 更新聚类中心 89 end_center = update_cluster_center(begin_center, assignment, k) 90 # 第二次分配样本 91 assignment = assign_points(data_points, end_center, k) 92 # 第二次的平方误差 93 end_sum_E = getE(assignment, end_center) 94 count = 2 # 计数器 95 #比较前后两个聚类中心向量是否相等 96 #print(compare(end_center,begin_center)==False) 97 while( begin_sum_E != end_sum_E): 98 begin_center=end_center 99 begin_sum_E=end_sum_E 100 # 再次更新聚类中心 101 end_center = update_cluster_center(begin_center, assignment, k) 102 # 进行分配 103 assignment = assign_points(data_points, end_center, k) 104 #计算误差 105 end_sum_E = getE(assignment, end_center) 106 count = count + 1 #计数器加1 107 return assignment,end_sum_E,end_center,count 108 def print_result(count,end_sum_E,k,assignment): 109 # 打印最终聚类结果 110 print(‘经过‘, count, ‘次聚类,平方误差为:‘, end_sum_E) 111 print(‘---------------------------------分类结果---------------------------------------‘) 112 for i in range(k): 113 print(‘第‘,i+1,‘类数据:‘,assignment[i]) 114 print(‘--------------------------------------------------------------------------------\n‘) 115 116 def plot(k, assignment,center): 117 #初始坐标列表 118 x = [] 119 y = [] 120 for i in range(k): 121 x.append([]) 122 y.append([]) 123 # 填充坐标 并绘制散点图 124 for j in range(k): 125 for i in range(len(assignment[j])): 126 x[j].append(assignment[j][i][0])# 横坐标填充 127 for i in range(len(assignment[j])): 128 y[j].append(assignment[j][i][1])# 纵坐标填充 129 plt.scatter(x[j], y[j],marker=‘o‘) 130 plt.scatter(center[j][0], center[j][1],c=‘b‘,marker=‘*‘)#画聚类中心 131 # 设置标题 132 plt.title(‘K-means Scatter Diagram‘) 133 # 设置X轴标签 134 plt.xlabel(‘X‘) 135 # 设置Y轴标签 136 plt.ylabel(‘Y‘) 137 # 显示散点图 138 plt.show() 139 140 def main(): 141 # 3个聚类中心 142 k = 4 143 data_points =read_data() 144 assignment, end_sum_E, end_center, count = k_means(data_points, k) 145 min_sum_E = 1000 146 #返回较小误差 147 while min_sum_E>end_sum_E: 148 min_sum_E=end_sum_E 149 assignment, end_sum_E, end_center, count = k_means(data_points,k) 150 print_result(count, min_sum_E, k, assignment)#输出结果 151 plot(k, assignment,end_center)#画图 152 main()
data文件数据:
2.0 4.2 2.1 5.0 2.3 3.8 1.2 6.1 3.5 4.4 3.6 3.7 3.0 6.2 2.5 5.6 1.7 3.3 0.9 6.0 0.4 4.1 7.0 10.0 8.0 9.0 8.2 8.2 9.3 7.9 7.4 7.1 6.8 8.0 8.1 9.5 8.5 10.4 7.6 8.5 8.6 7.3 7.7 8.8 1.8 10.9 1.5 9.5 1.7 8.7 1.3 9.0 2.8 9.6 2.2 9.9 2.1 10.5 2.5 9.2 3.1 10.4 3.9 9.5 3.7 10.4 2.6 8.2 2.8 9.2 2.2 9.3 3.4 8.5 8.1 1.3 8.5 2.4 8.8 3.3 9.0 1.2 10.7 2.9 7.9 3.7 7.5 2.5 8.5 0.6 10.8 1.6 9.2 0.5 6.8 2.0 8.5 3.6 10.0 1.7
原文:https://www.cnblogs.com/yby-algorithm/p/14016694.html