Jordan Lecture Note-6: The Solutions of Nonlinear Equation.

    本文主要介绍几种用于解非线性方程 $f(x)=0$ 的一些方法。

（1） Bisection Method.

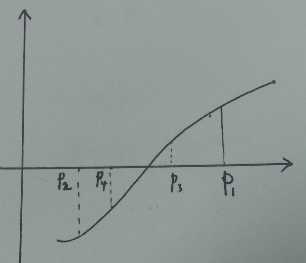
算法：

step 1: 初始化 $a,b(b>a)$ ，使 $f(a),f(b)$ 异号。

step 2: while (停止条件不满足)

                $p=a+\frac{b-a}{2}$ ；

                若 $f(p)f(a)<0$ ， $b=p$ ；否则 $a=p$ 。

           end while

step 3: 返回的 $p$ 为方程 $f(x)=0$ 的解。

 停止条件：

1. $$\begin{equation}|p_N-p_{N-1}|<\epsilon\label{equ:bisection1}\end{equation}$$ .
2. $$\begin{equation}\frac{|p_N-p_{N-1}|}{|p_N|}<\epsilon\label{equ:bisection2}\end{equation}$$
3. $$\begin{equation}|f(p_N)|<\epsilon\label{equ:bisection3}\end{equation}$$
   

 若采用式子 $\ref{equ:bisection1}$ 和 $\ref{equ:bisection2}$ 作为停止的判断标准，会产生一种情况，即 $\lim{n\to\infty}(p_n-p_{n-1})=0$ ，但序列 $\{p_n\}$ 却发散。即算法可能会停止与 $f(p_n)$ 不等与0处。如 $p_n=\sum_{k=1}^n\frac{1}{k}$ 。若采用式子 $\ref{equ:bisection3}$ 的判断标准，会产生一种情况，即 $|f(p_n)|<\epsilon$ ，但 $|p-p_n|$ 却很大。如 $f(x)=(x-1)^10$ ，当 $p_n=\frac{3}{2}$ 时 $|f(p_n)|<10^{-3}$ ，但实际上正确解与 $p_n$ 却相差 $\frac{1}{2}$ 。

 缺点：收敛太慢，为线性收敛。

（2） 固定点迭代(Fix-point iteration)。

定理：1）函数 $g$ 的定义域为 $[a,b]$ ，且对 $\forall x\in[a,b], g(x)\in [a,b]$ ，那么 $g$ 一定有fixed-point。

        2）在 $(a,b)$ 中 $g^\prime(x)$ 存在，且存在 $|g^\prime(x)|\leq k<1$ ，对 $\forall x\in (a,b)$ 成立，那么在 $[a,b]$ 内fixed-point唯一。

 证明：1）如果 $g(a)=a$ 或者 $g(b)=b$ ，定理 1）成立。否则 $g(a)>a,g(b)<b$ ，令 $h(x)=g(x)-x, h(a)=g(a)-a, h(b)=g(b)-b<0$ ，根据中值定理，必然存在 $p$ 使 $h(p)=g(p)-p=0$ 。

          2）假设 $p,q$ 都是固定点，则 $\exists\xi, \frac{g(p)-g(q)}{p-q}=g^\prime(\xi)$ 。因此：

$$|p-q|=|g(p)-g(q)|=|g^\prime(\xi)||p-q|\leq k|p-q|<|p-q|$$

于 $k<1$ 矛盾，故 $p=q$ 。

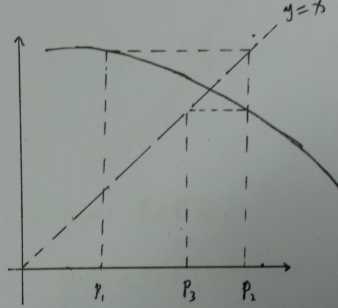
算法：

step 1: 初始化 $p_0,\epsilon,N_0$ ；

step 2: for $i=1,...,N_0$

                $p=g(p_0)$ ;

                if $|p-p_0|<\epsilon$

                     break;

                $p_0=p$ ;

           end for

step 3: 输出解 $p$ .

 例子：

如果要解决 $f(x)=x^3+4x^2-10=0$ 这个方程，则可转化成 $x=x+f(x)=x^3+4x^2+x-10$ 。

收敛分析：

满足在定义域 $[a,b]$ 内 $g(x)\in[a,b]$ ，并且 $|g^\prime(x)|\leq k<1$ ，那么固定点算法一定收敛。

证明：

迭代 $|p_n-p|\leq k^n(p_0-p)$ ，即 $\lim_{n\to\infty}|p_n-p|\leq \lim_{n\to\infty}k^n|p_0-p|=0$

其中 $k$ 的大小可以用来表示收敛的快慢，若 $k$ 接近与1，则收敛的慢；若 $k$ 接近于0则收敛的快。

（3）Newton-Raphson Method.

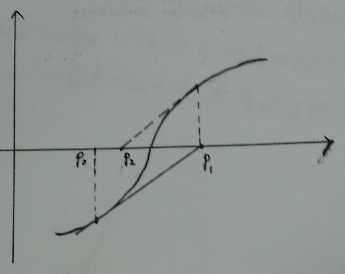
 从Taylor展开式看：

 其中 $\xi(x)$ 介于 $x$ 与 $\bar{x}$ 之间。所以：

由于 $|p-\bar{x}|$ 很小 $\Longrightarrow$ $|p-\bar{x}|^2$ 更小 $\Longrightarrow$ 故可以近似成：

从上式可以得到如下迭代式：

当 $f^\prime(p_{n-1})=0$ 时就无法进行。有定理证明Newton-Raphson 方法在区间 $[p-\delta,p+\delta]$ 内时一定会收敛到 $p$ ，但并未给出如何寻找这样的 $\delta$ 。

由于 $f^\prime(x)$ 往往很难计算，故提供一种计算 $f^\prime(x)$ 的近似方法。根据导数的定义: $f^\prime(p_{n-1})=\lim_{x\to p_{n-1}}\frac{f(x)-f(p_{n-1})}{x-p_{n-1}}$ 。

令 $x=p_{n-2}$ ，得到 $f^\prime(p_{n-1})=\frac{f(p_{n-2})-f(p_{n-1})}{p_{n-2}-p_{n-1}}$ ，故其对应的迭代式子：

这种方法称为正割法(Secant method)。从直观上看：

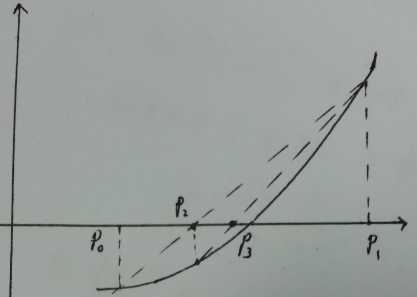
 根据Bisection方法的启示下可以得到一种新的迭代，称为试位法(False Position)。它的迭代式与Secant method一样，但在确定迭代式中的 $p_0$ 与 $p_1$ 时采用Bisection method中的方法，即保证新得到的点在 $p_0$ 与 $p_1$ 之间。

 （4）关于收敛.

定义：假定 $\{p_n\}_{n=0}^\infty$ 是一个收敛与 $p$ 的序列，且 $p_n\neq p$ ，如果存在正整数 $\lambda$ 和 $\alpha$ ，使

$$\lim_{n\to\infty}\frac{|p_{n+1}-p_n|}{|p_n-p|^\alpha}=\lambda$$ ，那么 $\{p_n\}_n^\infty$ 以order为 $\alpha$ 收敛于 $p$ ， $\lambda$ 为渐进错误。

当 $\alpha=1$ 时为线性收敛；

当 $\alpha=2$ 时为二次收敛。

 理解：

假设 $\{p_n\}_{n=0}^\infty$ 是线性收敛于0， $\lim_{n\to\infty}\frac{|p_{n+1}|}{|p_n|}=0.5$ ；若 $\{p_n\}_{n=1}^\infty$ 是二次收敛于0，则 $\lim_{n\to\infty}\frac{|p_{n+1}|}{|p_n|^2}=0.5$ 。很显然，二次收敛的速度要快于线性收敛。

Bisection method是线性收敛。Fixed-point iteration的收敛速度是根据函数 $g(x)$ 而定，最优的情况下可以达到二次收敛。Newton-迭代在初始值选择合理的情况下可以达到二次收敛，但若初始值不合理，可能使Newton迭代发散，所以通常较好的做法是先用Bisection迭代一定次数得到的值作为Newton迭代的初始值。Secant Method的迭代order $\alpha=1.62$ .

加速收敛：采用Aitken‘s $\Delta^2$ method加速收敛序列。

当 $n$ 足够大时，对 $\{p_n\}_{n=0}^\infty$ 有：

所以 $p_{n+1}^2-2p_{n+1}p+p^2\approx p_{n+2}p_n-(p_n+p_{n+2})p+p^2$

Aitken‘s $\Delta^2$ method 的迭代序列为：

大概的证明过程如下：

由 $\lim_{n\to\infty}\frac{p_{n+1}-p}{p_n-p}=\lambda$ 且 $\lim_{n\to\infty}\frac{\tilde{p_{n+1}}-p}{p_{n+1}-p}=0, \tilde{p_{n+1}}-p=\mathcal{O}(p_{n+1}-p)$

由于Aitken‘s $\Delta^2$ method 需要初始化三个值，故结合fixed-point method得到 Steffensen‘s method。初始化一个 $p_0^{(0)}, p_1^{(1)}=g(p_0^{(0)}), p_2^{(0)}=g(p_1^{(0)})$ ， 用Aitken‘s $\Delta^2$ method迭代式计算 $p_0^{(1)}$ ......

（5）Fisher Scoring迭代。

它是用于解决最大似然方程的一种迭代。由于Newton-Raphson迭代算法对初始值的要求很高，当初始值选的不合理时会产生震荡现象，导致算法无法收敛，而用Fisher Scoring迭代则解决了上诉问题。

使用Newton-Raphson求最大似然估计值，设log似然函数为 $l(\theta)$ ，

其梯度向量： $\nabla l(\theta^t)=[\frac{\partial l}{\partial \theta}]_{\theta^t}$ ;

海森矩阵： $H(\theta^t)=[\frac{\partial^2l}{\partial\theta_i\partial\theta_j}]_\theta^t$

$l(\theta)$ 在 $\theta^t$ 处的泰勒展开：

求导： $\frac{\partial l}{\partial\theta}=\nabla l(\theta^t)+H(\theta^t)(\theta-\theta^t)=0$

$\Longrightarrow \theta^{t+1}=\theta^t-[H(\theta^t)]^{-1}\nabla l(\theta^t)$

上述方法的缺点：

1. 计算量太大，主要是要计算嗨森矩阵。
2. 当 $H(\theta^t)$ 不可逆，或 $|H(\theta^t)|\approx 0$ 时，会产生震荡现象。当 $\theta^t$ 在 $\theta^*$ 附近处 $H(\theta^t)$ 很小，则 $\theta^{t+1}=\theta^{t}-\frac{dl/d\theta}{H(\theta^t)}$ 会变化很大。
   

Jordan Lecture Note-6: The Solutions of Nonlinear Equation.

原文：http://www.cnblogs.com/boostable/p/lec_solutions_of_nonlinear_equation.html