①\(BC\perp AD\);
②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\);
③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);
⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\);
⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\);
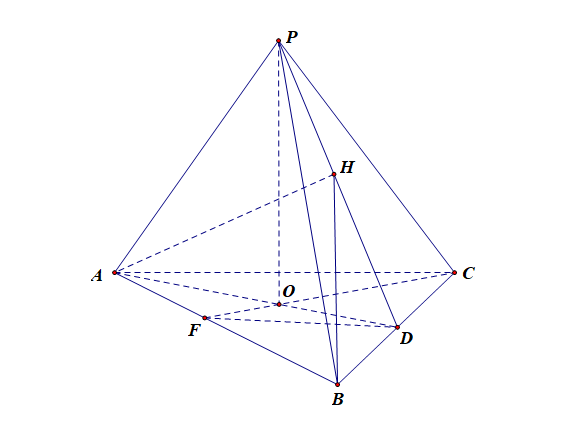
解析:本题目的信息量有点太大,具体解析如下,
①\(BC\perp AD\);
分析:由于点 \(A\) 在侧面 \(PBC\) 上的射影为 \(H\),故\(AH\perp\)平面\(PBC\),由于\(BC\subsetneqq PBC\),故\(AH\perp BC\);
又由于\(H\) 是 \(\triangle PBC\) 的垂心,故\(PD\perp BC\),
由\(BC\perp AH\),\(BC\perp PD\),且又\(AH\),\(PD\subsetneqq\) \(PAD\)、\(AH\cap PD=H\),
则\(BC\perp\)平面\(PAD\),又\(AD\subsetneqq\) \(PAD\),则得到\(BC\perp AD\);故①成立;
②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\);
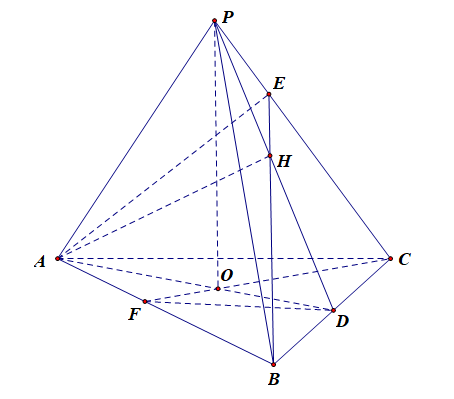
分析:如图所示,延长\(BH\)交\(PC\)于点\(E\),连结\(AE\),
则由\(AH\perp PC\),\(BE\perp PC\)(垂足),\(AH\cap BE=H\),\(AH\)、\(BE\subsetneqq\) \(ABE\),
故\(PC\perp\)面\(ABE\),\(AB\subsetneqq\)面\(ABE\),
则有\(PC\perp AB\),又\(PO\perp AB\),\(PC\cap PO=P\),\(PC\)、\(PO\subsetneqq\) \(POC\),
则\(AB\perp POC\),\(CO\subsetneqq\)面\(POC\),
则得到\(AB\perp CO\),则\(AB\perp CF\),
故\(O\)为\(\triangle ABC\)的垂心,又由于三角形为正三角形,
故\(O\)是\(\triangle ABC\)的中心,
故\(P-ABC\)为正三棱锥。
故可知,点\(D\),\(F\)分别为中点,连结\(PF\),则可得到\(PF\perp AB\),
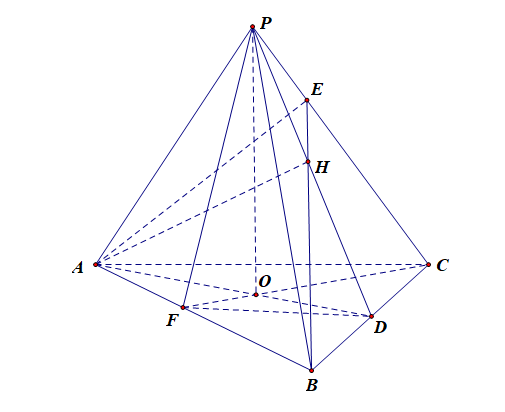
则\(\angle PFC\)为二面角 \(P-AB-C\) 的平面角。故②错误;
③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
分析:连结\(EF\),由①②可知,\(AB\perp\)平面\(PCF\),故\(AB\perp EF\),又\(PC\perp\)平面\(ABE\),故\(PC\perp EF\),
故线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线,又由于\(CF\perp AB\),
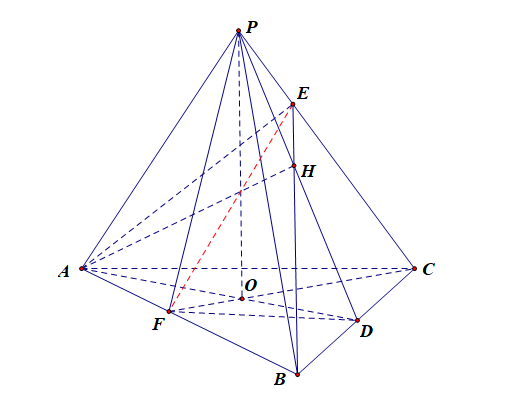
故\(\angle EFC\)为二面角\(H-AB-C\)的平面角,则由已知得\(\angle EFC=\cfrac{\pi}{6}\).
设正三角形\(ABC\)的边长为\(2x\),则\(BD=FB=x\),则\(CF=\sqrt{3}x\),
在\(Rt\triangle CEF\)中,由于\(\angle CFE=\cfrac{\pi}{6}\),故\(CE=\cfrac{\sqrt{3}}{2}x\),\(EF=\cfrac{3}{2}x\);
在\(Rt\triangle CEB\)中,可得\(BE^2=BC^2-CE^2=(2x)^2-(\cfrac{\sqrt{3}}{2}x)^2=\cfrac{13}{4}x^2\),
且由于是正三棱锥,有\(BE=AE\);
又在\(Rt\triangle PAF\)中,则\(PF^2==PA^2-AF^2=2^2-x^2=4-x^2\),
则在\(Rt\triangle PEF\)中,\(PE^2=PF^2-EF^2=4-x^2-\cfrac{9}{4}x^2=4-\cfrac{13x^2}{4}\),
由已知\(PA=2=PC\),即\(PE+CE=PC=2\),即\(\sqrt{4-\cfrac{13x^2}{4}}+\cfrac{\sqrt{3}}{2}x=2\),
移项,得到\(\sqrt{4-\cfrac{13x^2}{4}}=2-\cfrac{\sqrt{3}}{2}x\),两边平方,解得\(x=\cfrac{\sqrt{3}}{2}\),
故可得\(AB=BC=AC=\sqrt{3}\),\(BD=BF=\cfrac{\sqrt{3}}{2}\),\(AD=\cfrac{\sqrt{3}}{2}\times\sqrt{3}=\cfrac{3}{2}\),
则由点\(O\)为正三角形\(ABC\)的重心,得到\(AO=\cfrac{3}{2}\times \cfrac{2}{3}=1\),
在\(Rt\triangle PAO\)中,\(PA=2\),\(AO=1\),故\(\angle PAO=\cfrac{\pi}{3}\).
即直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);
分析:由上可知,线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线,

且\(EF=\cfrac{3}{2}x=\cfrac{3}{2}\times\cfrac{\sqrt{3}}{2}=\cfrac{3\sqrt{3}}{4}\);
即两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);故④正确;
⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\);
分析:由于点\(D\), \(F\)分别是线段\(BC\)和\(AB\)的中点,故\(DF//AC\),
则直线 \(FD\) 与直线 \(PC\) 所成角的也就是直线 \(AC\) 与直线 \(PC\) 所成的角,
由上可知是正三棱锥,故在\(\triangle PAC\)中,\(PA=PC=2\),\(AC=AB=BC=\sqrt{3}\),
故由余弦定理或者构造\(Rt\triangle\)可得到,\(\cos\angle PCA=\cfrac{\sqrt{3}}{4}\),故④错误;
⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\);
分析:由上可知,\(PC=2\),\(CD=\cfrac{\sqrt{3}}{2}\),则\(PD^2=PC^2-CD^2=2^2-(\cfrac{\sqrt{3}}{2})^2=\cfrac{13}{4}\),
则\(PO^2=PD^2-OD^2=\cfrac{13}{4}-\cfrac{1}{4}=3\),即\(PO=\sqrt{3}\),
故\(V_{P-ABC}=\cfrac{1}{3}\cdot S_{\triangle ABC}\cdot PO=\cfrac{1}{3}\cdot \cfrac{\sqrt{3}}{4}\cdot(\sqrt{3})^2\cdot \sqrt{3}=\cfrac{3}{4}\),故⑥正确,
综上所述,正确的命题有:①③④⑥;
原文:https://www.cnblogs.com/wanghai0666/p/14004975.html