高斯消去法,其实就是利用初等变换把矩阵转换成上三角,便于求行列式,求逆,求线性方程组的解
其实核心代码特别短,如下
void elimination(double *matrix, int row, int column) { for (int i = 0; i < column - 1; i++) { for (int j = 0; j < row - 1 - i; j++) { double coef = *(matrix + (row - 1 - j)*column + i) / *(matrix + i * column + i); for (int k = 0; k < column; k++) { *(matrix + (row - 1 - j)*column + k) -= (coef*(*(matrix + i * column + k))); } } } }
用主函数测试一下正确性
int main() { // double matrix[] = { 1,2,3,4,5,6,7,8,9 }; double matrix[] = { 1,1,-1,2,1,0,1,-1,0 }; int row = 3, column = 3; printf("------原矩阵------\n"); // int i, j; for (int i = 0; i < row; i++) { for (int j = 0; j < column; j++) { printf("%4lf ", *(matrix + i * row + j)); } printf("\n"); } elimination(matrix, row, column); printf("------结果------\n"); for (int i = 0; i < row; i++) { for (int j = 0; j < column; j++) { printf("%4lf ", *(matrix + i * row + j)); } printf("\n"); } return 0; }
结果如下,显然正确
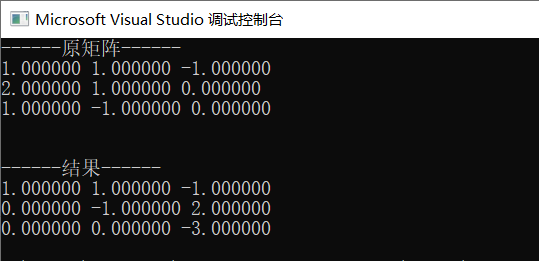
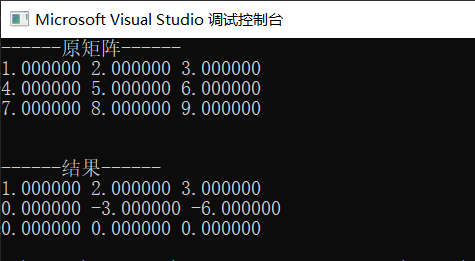
原文:https://www.cnblogs.com/zhaoke271828/p/14001337.html