ALG 3-2: Graph Connectivity & Graph Traversal (BFS)

Connectivity

s-t connectivity problem. Given two node s and t, is there a path between s and t?

(s - t连接问题:  给定两个节点s和t，在s和t之间有路径吗?)

s-t shortest path problem. Given two node s and t, what is the length of the shortest path between s and t?

(s-t最短路径问题:  给定两个节点s和t,  s和t之间的最短路径的长度是多少?)

Applications.

• Friendster. (交友网站)
• Maze traversal. (迷宫遍历)
• Kevin Bacon number. (凯文·培根数)
• Fewest number of hops in a communication network. (在一个通信网络中最少的跳转数)

Breadth First Search （广度优先搜索）

BFS intuition. Explore outward from s in all possible directions, adding nodes one "layer" at a time.

（BFS的核心思想: 从s节点向外探索所有可能的方向，一次添加一个“层”节点。）

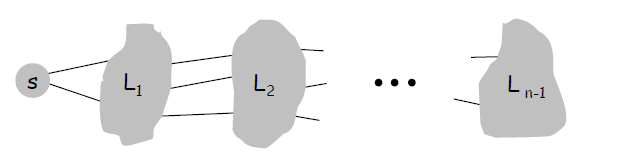
BFS algorithm.

• L0 = { s }.
• L1 = all neighbors of L0.
• L2 = all nodes that do not belong to L0 or L1, and that have an edge to a node in L1.
• ( L2 = 所有不属于L0或L1的节点，并且与L1中的节点有一条边的节点）
• Li+1 = all nodes that do not belong to an earlier layer, and that have an edge to a node in Li.
• ( Li+1 = 不属于前一层的所有节点，并且与Li中的某个节点有一条边)

Theorem. For each i, Li consists of all nodes at distance exactly i from s. There is a path from s to t iff t appears in some layer. 

(定理: <1>对于每一个i, Li由距离s正好i的所有节点组成  <2> 存在一条从s到t的路径当且仅当t出现在某个层中)

Property. Let T be a BFS tree of G = (V, E), and let (x, y) be an edge of G. Then the level of x and y differ by at most 1.

(特性: 设T是G = (V, E)的BFS树，设(x, y)是G的一条边，那么x和y的级别相差不超过1)

Breadth First Search: Analysis

Theorem. The above implementation of BFS runs in O(m + n) time if the graph is given by its adjacency representation.

(定理：如果图是用邻接的方式表示的，那么上述BFS的实现在O(m + n)时间内运行)

Pf.

• Easy to prove O(n^2) running time:

  • at most n lists L[i]
    each node occurs on at most one list; for loop runs ≤n times (每个节点最多出现在一个列表上;for循环运行≤n次)
    when we consider node u, there are ≤n incident edges (u, v),and we spend O(1) processing each edge (考虑节点u时，有≤n条关联边(u, v)，对每条边进行O(1)处理)

• Actually runs in O(m + n) time:
  • when we consider node u, there are deg(u) incident edges (u, v)　//考虑节点u时，存在deg(u)个关联边(u, v)
  • total time processing edges is Σu∈V deg(u) = 2m (each edge (u, v) is counted exactly twice)
  • (总时间处理边Σu∈V deg(u) = 2m (每条边(u, V)精确计数两次) )

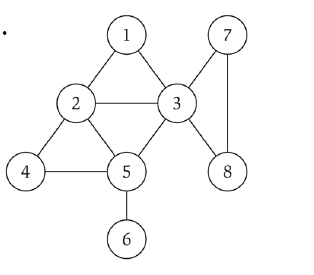
Connected Component

Connected component. Find all nodes reachable from s.

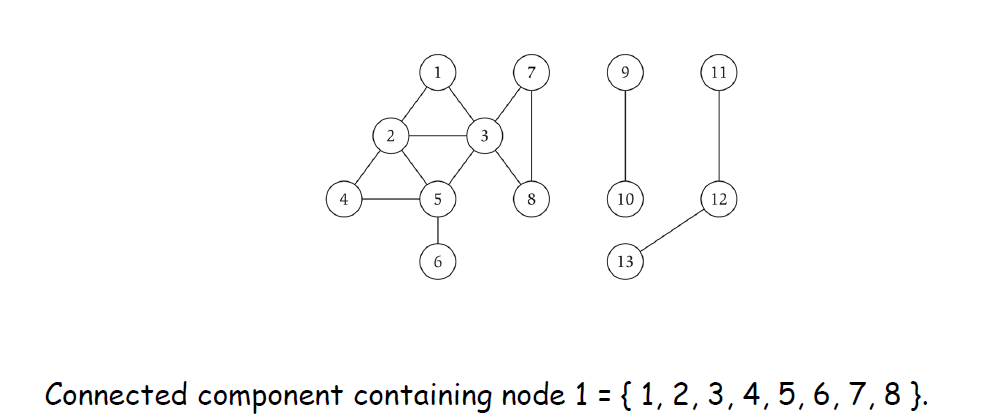
Theorem. Upon termination, R is the connected component containing s. // 在终止时，R是包含s的 "连通组件"

• BFS = explore in order of distance from s. (按距离s的顺序探索)
• DFS = explore in a different way.

ALG 3-2: Graph Connectivity & Graph Traversal (BFS)

原文：https://www.cnblogs.com/JasperZhao/p/13975603.html