P VS NP

1.1 P

Def. Algorithm A runs in polynomial time if for every string s, A(s)
terminates in ≤ p( ?s?) “steps,” where p(?) is some polynomial function.

在多项式时间内可以求解的问题就是P类问题。

1.1.1 NP

Def. Algorithm C(s, t) is a certifier for problem X if for every string s : s ∈ X iff there exists a string t such that C(s, t) = yes.
NP = set of decision problems for which there exists a poly-time certifier.
?C(s, t) is a poly-time algorithm.
?Certificate t is of polynomial size: ?t? ≤ p(?s?) for some polynomial p(?)

在多项式时间内可以验证一个解的问题就是NP问题。

关于NP举一个例子：

• 我们找是否有两个数相乘等于437669
• 首先我们找到了一个可验证的解就是541
• 那么只要我们可以找多项式时间内找到809我们就可以找到原问题的解。

1.1.2 Certifiers and certificates: satisfiability

• 3-SAT. SAT where each clause contains exactly 3 literals.
• Certificate. An assignment of truth values to the Boolean variables.
• Certifier. Check that each clause in Φ has at least one true literal.

可满足性问题和三元可满足性问题都属于NP问题,我们不一定在多项式时间里找到全部解但是我们可以在多项式时间内验证一个解的成立！

验证步骤是这样的：

1. 首先我们找到其中一个解作为验证实例比如x1=true,x2=tru2,x3=false,x4=false;
2. 我们必须在多项式时间内可以验证这个解是成立的！

2.1 Certifiers and certificates: Hamilton path

HAMILTON-PATH： Given an undirected graph G = (V, E), does there exist a
simple path P that visits every node?

Certificate： A permutation π of the n nodes.

Certifier： Check that π contains each node in V exactly once,
and that G contains an edge between each pair of adjacent nodes

哈密尔顿圈问题是一个NP问题，我们可以很容易找到一个解比如包含全部结点的路径并在多项式时间内验证解成立！
ps:简单路径：指图G(V，E)中路径上的顶点都不相同的路径。

2.1.1 Some problems in NP

3.1 P, NP, and EXP

P. Decision problems for which there exists a poly-time algorithm.
NP. Decision problems for which there exists a poly-time certifier.
EXP. Decision problems for which there exists an exponential-time algorithm.

EXP是指一个问题在指数级时间内存在解。

3.1.1 The main question: P vs. NP

Does P = NP? [Cook 1971, Edmonds, Levin, Yablonski, G?del]
Is the decision problem as easy as the certification problem?

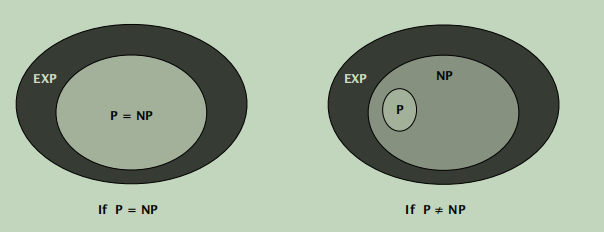
If yes… Efficient algorithms for 3-SAT, TSP, VERTEX-COVER, FACTOR, …
If no… No efficient algorithms possible for 3-SAT, TSP, VERTEX-COVER, …

P VS NP

原文：https://www.cnblogs.com/xhj928675426/p/13973151.html