例题:
题目描述
迷宫用 n*mn?m 的网格表示,分为以下四种格子:
X:墙,不能通过
.:空地,可以通过
^:陷阱(开启):可以通过,但行动后如果处在开启的陷阱上上会额外消耗1点体力
_:陷阱(关闭):可以通过
每次你可以从当前格子花费1点体力进行一次行动,包括移动到上下左右四方向的某一个可以通过的格子,或者停留在原地。
在每次行动时,所有陷阱的状态会在开启和关闭之间切换。如果相邻格子当前为一开启的陷阱,当你移动到上面时它会关闭,所以不会额外消耗体力。反之如果相邻一个当前关闭的陷阱,则移动到上面需要额外消耗1体力。
你的起点为迷宫左上角,终点为迷宫右下角,你需要找到一个消耗体力值最少的行动方法。
保证起点和终点处为空地。
输入格式
第一行两个整数n, mn,m,分别表示迷宫的行数和列数
接下来nn行mm列,每个字符代表一个格子,见题目描述,表示开始时迷宫的状态
输出格式
一行一个整数,表示最少消耗的体力
输入输出样例
输入 #1
5 5
.....
^XXX.
_X...
.X.XX
^....
输出 #1
9
显然,走的步数是奇数步时,地图状态都一样;走了偶数步时,地图状态也都一样。在没有陷阱的情况下,我们可以通过建一个两层的二维图,第一层为偶数层(因为从0步开始,0为偶数),第二层为奇数层。每走一步,就去到另一个层的对应点,如图:
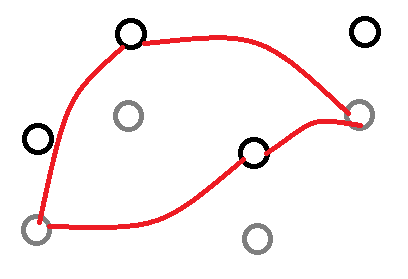
当有陷阱时,我们有两种决策,第一种是做一次停留,另一种是踩进陷阱并因此额外耗费一点体力。
当停留时,位置没有改变,但是因为停留也是一种行动,步数的奇偶性仍会发生改变,因此,在二维图中,所处的维度会去到另一层,如图:
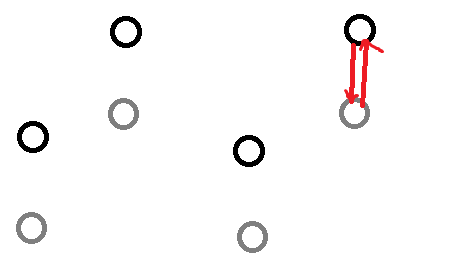
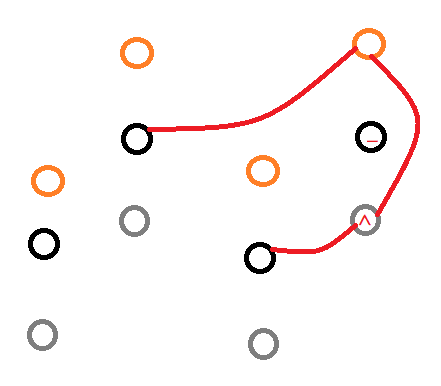
当踩入陷阱时,会额外耗费一点体力,相当于做了一次行动却耗费了两点体力,那么,我们可以通过建立一个第三维度,当在所处维度踩到陷阱时,再耗费一点体力去到第三维度的对应位置,然后从第三维度的对应位置再耗费一点体力去到下一个对应的维度。因为在同一个陷阱上停留是没有意义的,所以不考虑第三维度的停留问题。
当在偶数维度踩到陷阱时,建立一条从当前的点到第三维度对应点的边,再建立一条从第三维度对应点到奇数维度下一个点的边,用来等效额外的体力消耗。奇数维度时如法炮制。
如图:
代码实现:
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
using namespace std;
const int maxn=510;
int n,m,pow[maxn*maxn*3],dx[4]={-1,1,0,0},dy[4]={0,0,-1,1},ed0,ed1,ans;
vector <int> e[maxn*maxn*3];
queue <int> q;
char str[maxn][maxn];
void ist(int u,int v)
{
e[u].push_back(v);
}
void bfs()
{
q.push(0);
while(!q.empty())
{
int t=q.front();
q.pop();
if(t==ed0 || t==ed1) return;//只要第一次到达了终点,那么此时体力耗费一定最小
for(int i=0;i<e[t].size();i++)
{
int to=e[t][i];
if(pow[to]<0)
{
pow[to]=pow[t]+1;
q.push(to);
}
}
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
scanf("%s",str[i]);
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
int s0=(i*m+j)*3,s1=s0+1;//将三维坐标压缩成一维坐标
if(str[i][j]==‘X‘) continue;
ist(s0,s1),ist(s1,s0);//在s0和s1之间建一条双向边,因为在任意状态都可以停留
if(str[i][j]==‘^‘)
{
ist(s0,s0+2);
//在走了偶数步时踩到陷阱,还需要在在偶数维度和第三维度之间建一条单向边,等效替代踩到陷阱时多消耗的体力
//在同一个陷阱上消耗两次体力是没有意义的,所以只建单向边
s0+=2;//去到第三维度
}
if(str[i][j]==‘_‘)
{
ist(s1,s1+1);//走了奇数步踩到陷阱,在奇数维度和第三维度之间建一条边
s1++;//去到第三维度
}
for(int k=0;k<4;k++)
{
int mx=i+dx[k],my=j+dy[k];
if(mx<0 || mx>=n || my<0 || my>=m || str[mx][my]==‘X‘) continue;
int t0=(mx*m+my)*3,t1=t0+1;
ist(s0,t1),ist(s1,t0);//当前是奇维度,下一步就走向偶维度;反之亦然
}
}
}
ed0=((n-1)*m+m-1)*3,ed1=ed0+1;//终点的一维坐标
memset(pow,-1,sizeof(pow));
pow[0]=0;
bfs();
if(pow[ed0]>0 && pow[ed1]>0) ans=min(pow[ed0],pow[ed1]);
else if(pow[ed0]>0) ans=pow[ed0];
else ans=pow[ed1];
printf("%d\n",ans);
return 0;
}原文:https://www.cnblogs.com/SeekHummingbird/p/13972429.html