设F是一个森林,B是由F转换得到的二叉树,F中有n个非终端节点,则B中右指针域为空的节点有______个?
答案是n+1
首先F是一个森林,未规定森林中树的度,就是里面可能有任意叉的树。
要把森林转换成二叉树,首先得把森林中的树一个一个转换成左子右兄弟表示的二叉树,再把它们接到一起。
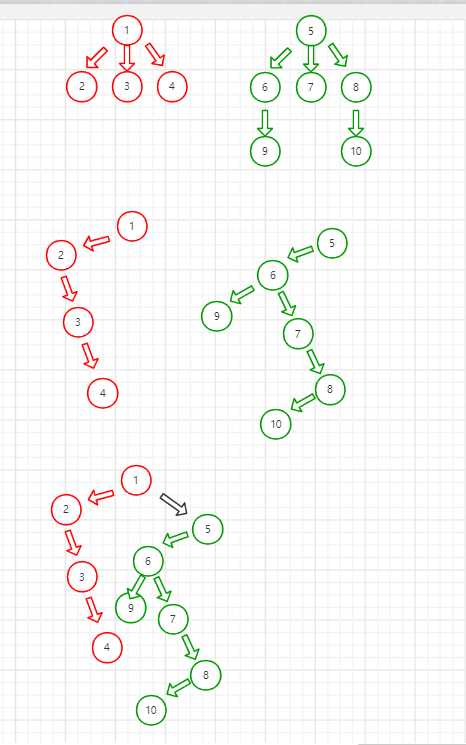
就这样接。第一层代表森林中的树,第二层代表森林中的树都转换成左子右兄弟表示,第三层代表把这些转换过的树合成一个新二叉树。记住,原森林中有4个非终端节点,1,5,6,8,这就是题目中的n。
按照左子右兄弟的定义,转换成二叉树后没有右子节点就代表它在原树中是一排亲兄弟中最右的那一个,或者是根节点。
下图中的黑色节点代表的就是这种节点。
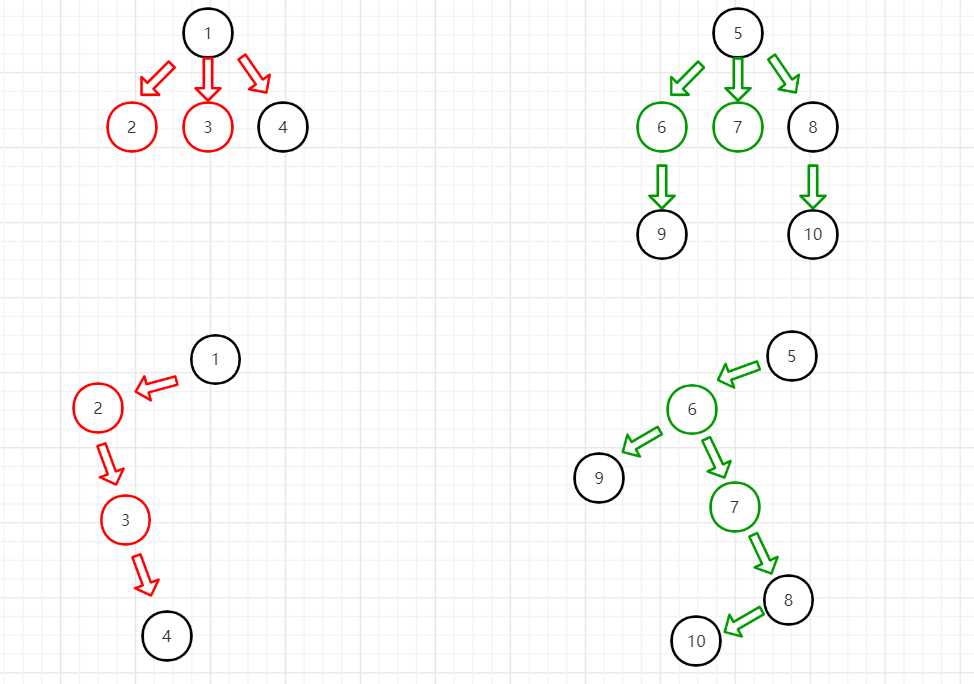
按照定义把这些森林连接成树之后,就只剩下森林中最后一棵树没有右子节点。
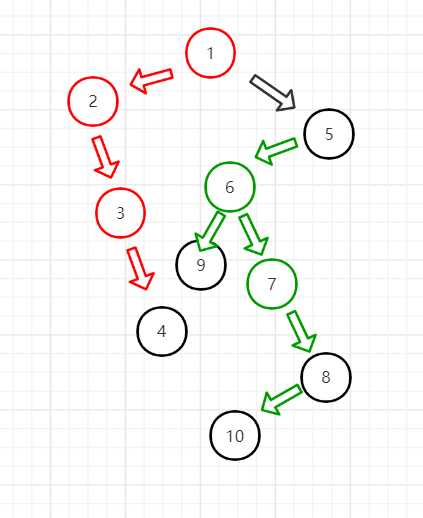
有了这些知识,我们就可以考虑n+1这个答案是怎么来的了。
我们知道最后合成的树中的没有右子节点的节点来自于原树中的亲兄弟的最右兄弟和最后被接的树的根,而原树中有n个非终端节点,也就是非叶子节点,每个非叶子节点都会有若干个孩子,这些孩子里必定有一个排在最右,也就是我们之前说的最右兄弟,那么也就是说,原树中有n个节点,合成的二叉树中就会有n个节点无右子节点,再加上最后合并的树的树根无右子节点,所以答案就是n+1
原文:https://www.cnblogs.com/lilpig/p/13940585.html