周练（10）64. 最小路径和

• 注意，Python初始化一个二维数组，不能用 [[0] * col] * row，这样每行创建的是 [0]*col的引用！！！！！！

• 使用 [[0] * col for _ in range(row)]

#
# @lc app=leetcode.cn id=64 lang=python3
#
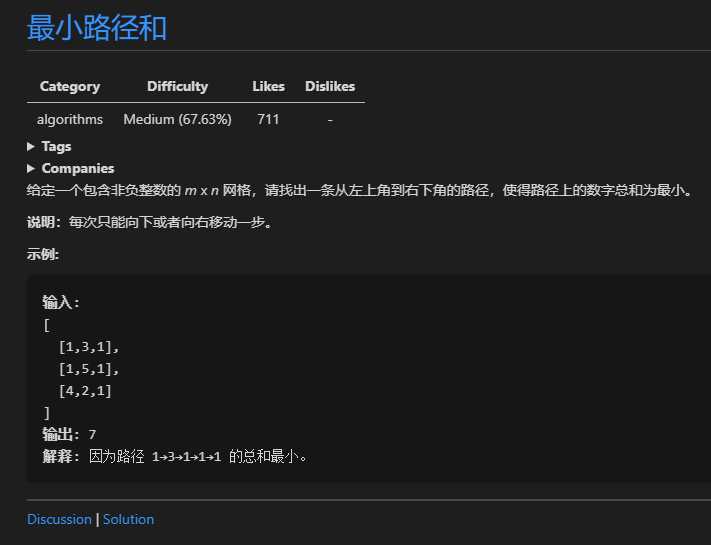
# [64] 最小路径和
#

# @lc code=start
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        # 1. 状态设置
        #  - 令dp[i][j] 代表从(i, j) 点走到(m-1, n-1)点的最小路径和.
        # 2. 状态转移方程
        #  - 如何求出dp[i][j]。由于每次只能往右或下走，所以从(i,j)只能走到
        #  - (i+1, j)或者(i, j+1)。
        #  - 换言之，dp[i][j]的前继状态只有dp[i+1][j], dp[i][j+1]
        #  - 所以，我们在两者之间取最小，然后加上这个格子内的数即可
        # dp(i,j) = grid(i,j) + min(dp(i-1,j), dp(i, j-1))
        row, col = len(grid), len(grid[0])
        if row == 0 or col == 0:
            return 0
        dp = [[0] * col for _ in range(row)]
        dp[0][0] = grid[0][0]

        # 当 i>0 且 j=0 时，dp[i][0] = dp[i-1][0] + grid[i][0]
        # 当 i=0 且 j>0 时，dp[0][j] = dp[0][j - 1] + grid[0][j]
        # 当 i>0 且 j>0 时，dp[i][j] = grid[i][j] + min(dp[i+1][j], dp[i][j+1])
        for i in range(1, row):
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for j in range(1, col):
            dp[0][j] = dp[0][j-1] + grid[0][j]
        
        for i in range(1, row):
            for j in range(1, col):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
        
        print(dp)
        return dp[row - 1][col - 1]
# @lc code=end

周练（10）64. 最小路径和

原文：https://www.cnblogs.com/douzujun/p/13935878.html