题目链接:K. PepperLa‘s Boast
题意:给你一个n * m的矩阵,你要从(1, 1)点走到(n, m)点,由于矩阵着火,你每次只能往右,往下,往右下其中一个方向走1步,矩阵每个点有a[i][j]那么多的空气,如果a[i][j]<=0,则该点充满烟雾你在该点不能呼吸,每次呼吸你可以吸入任意数量的空气并存下来,在经过烟雾点时,你必须憋气,每次憋气花费U的气体走最多K步,问你是否可以走到点(n, m),如果可以输出最终肺内最多能剩余多少气体,如果不能输出-1
Input
多组输入,每组输入N,M,K,U(1≤N,M≤1e3,1≤K,U≤1e9) 表示n*m的矩阵,K代表走最多K步,U代表每次憋气需要花费U那么多气体,然后输入n * m的矩阵,a[i][j]∈[?1e9,1e9],∑n*m<=7e6,输入保证a[1][1], a[n][m]>0
Output
问你是否可以走到点(n, m),如果可以输出最终肺内最多能剩余多少气体,如果不能输出-1
Sample Input
3 4 2 1
1 0 0 9
0 -1 1 1
-1 0 2 1
Sample Output
4
思路:考虑dp,dp[i][j]表示到点(i, j)时肺内最多剩余多少气体,点(i, j)要么由不憋气走一步,要么由憋气走最多K步转移过来,所以dp[i][j]的状态转移方程为
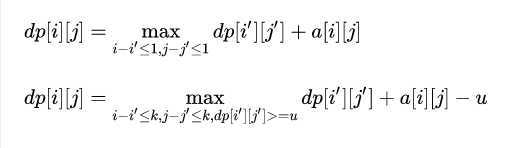
问题转化为求以点(i, j)为矩阵右下角的长宽为K的矩阵极值
我们用递减单调队列来维护区间极值,对于每一列建一个递减单调队列,从左往右扫的时候用一个行的单调队列维护区间极值,入队的是列单调队列的队首元素

#include<bits/stdc++.h> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int N = 1010; struct node { ll data; int id; }; int n, m, k, u; int a[N][N]; ll dp[N][N]; node row[N], col[N][N]; int head1, tail1; int head[N], tail[N]; int main() { for(int i = 0; i < N; i++) dp[i][0] = dp[0][i] = -1; while(~scanf("%d %d %d %d", &n, &m, &k, &u)) { for(int i = 1; i <= m; i++) head[i] = tail[i] = 0; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { scanf("%d", &a[i][j]); dp[i][j] = -1; } } dp[1][1] = a[1][1]; for(int i = 1; i <= n; i++) { head1 = tail1 = 0; for(int j = 1; j <= m; j++) { while(head[j] < tail[j] && col[j][head[j]].id < i - k) head[j]++; while(head1 < tail1 && row[head1].id < j - k) head1++; if(a[i][j] > 0) { if(dp[i - 1][j] != -1) dp[i][j] = max(dp[i][j], dp[i - 1][j] + a[i][j]); if(dp[i][j - 1] != -1) dp[i][j] = max(dp[i][j], dp[i][j - 1] + a[i][j]); if(dp[i - 1][j - 1] != -1) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + a[i][j]); if(head[j] < tail[j]) { ll now = col[j][head[j]].data; while(head1 < tail1 && row[tail1 - 1].data <= now) tail1--; row[tail1++] = (node){now, j}; } if(head1 < tail1) dp[i][j] = max(dp[i][j], row[head1].data + a[i][j] - u); if(head[j] < tail[j]) tail1--; } if(dp[i][j] >= u) { while(head[j] < tail[j] && dp[i][j] >= col[j][tail[j] - 1].data) tail[j]--; col[j][tail[j]++] = (node){dp[i][j], i}; } if(head[j] < tail[j]) { ll now = col[j][head[j]].data; while(head1 < tail1 && row[tail1 - 1].data <= now) tail1--; row[tail1++] = (node){now, j}; } // cout << i << " " << j << " " << dp[i][j] << endl; } } printf("%lld\n", dp[n][m]); } return 0; }
PepperLa's Boast(dp+二维单调队列维护区间极值)
原文:https://www.cnblogs.com/lsl127/p/13916691.html