SVM是一种用于二分类问题的监督学习算法,由Vapnik等人在1995年提出。
Decision Boundaries的划分有多种方法:Neural Networks、Nearest Neighbors以及SVM等等,当一种方法无法继续时,我们要考虑用新的视角去解决问题。
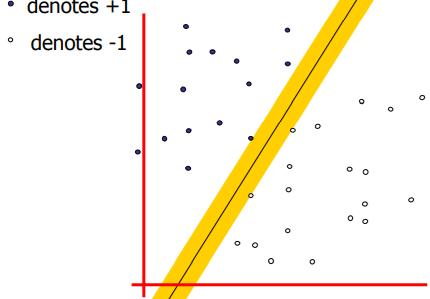
我们的基本问题是:在线性可分的情况下,用哪条直线来区分正负样本效果最好呢?

SVM的思想是找到一条有着maximum margin的线,MIT的课里叫做widest street approach:
引入垂直于street的长度未知的向量\(w\),对于任意一个样本点\(u\),我们希望判断出它的正负,那么我们只要计算出\(u\)在\(w\)方向上的投影,即如果\(w\cdot u \geq c\),那么就可以判断为正样本,稍作改写即可得到Decision Rule:
接下来的问题就是计算\(b\)和\(w\),需要添加约束条件,我们认为对于正负样本:
这样正负样本之间就有一个距离间隔。
为了统一表示上面2种情况,引入\(y_i=\begin{cases}
1,&\text{+sample}\-1,&\text{-sample}
\end{cases}\),所有样本统一表示为:
对于street边缘的点(support vectors),等号成立:$$y_i(w\cdot x_i+b)-1=0\tag{2}$$
为了求出最佳直线(street宽度最大),首先要表示出宽度:
取一个正样本的support vector\(x_+\)以及一个负样本的support vector\(x_-\),那么宽度就是\(x_+-x_-\)在\(w\)方向上的投影:
接下来就是要在约束条件(2)下求得(3)的最大值,也即最小化\(\frac{||w||^2}{2}\),这种问题叫做Quadratic Optimization Problem。
约束条件下的极值问题自然要想到Lagrange Multiplier:
分别对\(\vec{w}\)和\(b\)求偏导:
决策向量\(\vec{w}\)是样本的线性和,将\(\vec{w}\)代入\(L\),看看我们的极值会变成什么:
到这里,我们发现了一个令人惊喜的结论:我们的极值只依赖于样本对之间的点积。
再将\(\vec{w}\)代入Decision Rule(1),有:
类似地,Decision Rule也只取决于样本点和未知点的点积。
与神经网络不同,这里的优化问题是凸优化,意味着不会卡在局部最大,一定可以找到全局最优解。
上面我们讨论了线性可分的情况,如果线性不可分呢?
当前的特征空间线性不可分,我们可以做一个变换\(\phi(\vec{x})\),将样本映射到另外一个空间,也许就线性可分了。(4)式表明最值只依赖于点积,所以变换后的优化同样只需要最大化\(\phi(\vec{x_i})\cdot\phi(\vec{x_j})\),只要有一个函数\(K(\vec{x_i},\vec{x_j})=\phi(\vec{x_i})\cdot\phi(\vec{x_j})\)提供新空间的样本点的点积,我们都不需要知道这个变换是什么,就可以得到最优解,\(K\)叫做Kernel Function。
一种常用的kernel是线性的:\((\vec{u}\cdot\vec{v}+1)^n\),当前空间的\(u\)和\(v\)通过简单的点积映射到了另一个空间;
另一种kernel是高斯核:\(e^{-\frac{||x_i-x_j||}{\sigma}}\)。
原文:https://www.cnblogs.com/EIMadrigal/p/13913864.html