在线搜索(一)中,我们介绍了如何确定搜索的步长,以确保每次迭代都能获得更接近最优值的结果。本文,我们转而从更宏观的角度考察,看看不同的线搜索方法在收敛性和收敛速度上有哪些差异,他们是否都能收敛,谁的收敛速度更快?考察的对象是之前提到过的三种线搜索方法:最速下降法、牛顿法、拟牛顿法。
如何定义“收敛”?很简单,函数值到达极值点就叫做收敛。因为在极值点处,导数为0,向任何方向的移动都不会使函数值变化。即
那么,接下来需要研究的就是,如何选择方向,可以保证上式成立。
假设我们选择的方向为 ,定义
与梯度下降方向的夹角为
,即
为了顺利推导出符合(3.18)要求的方向,我们需要对目标函数的导数做个限制,要求其具有Lipschitz continuous性质,即
这一性质可以理解为导数不能变化得太快,可以想象,如果不做任何限制,函数值的剧烈变化会导致收敛变得非常困难。好在实际应用中,该性质一般都是成立的。
在Lipschitz continuous性质的约束下,如果每次迭代的步长都满足上一篇文章提到的Wolfe conditions,我们就可以推导出下面的结果
推导过程并不重要,重要的是这个不等式有什么含义。它告诉我们,当迭代次数足够多时,要么 趋近于90°,要么梯度
趋近于0。
现在,我们分情况考虑。
在最速下降法中, 永远等于0°,因为我们直接选取了梯度的反方向作为优化方向。这样的话,式(3.16)就意味着
必然趋近于0。稍微回头看一下式(3.18),就会发现这恰好意味着收敛。也就是说,最速下降法必然会收敛。
再考虑牛顿法和拟牛顿法。这两种方法选择的优化方向为
其中, 是目标函数的二阶导或二阶导的近似,一般称作海森矩阵。对于凸函数来说,该矩阵是对称半正定矩阵,其对称性质由其定义可得,其半正定性质可由凸函数的定义推导得出。
接下来,我们试试能否通过这些条件推导出式(3.18)的结果,从而证明牛顿法和拟牛顿法也是收敛的。思路很简单,仍然是证明 不趋近于0,从而间接证明
必须趋近于0。
不趋近于0意味着
我们需要找出符合要求的 。证明的过程仍然比较复杂,需要综合式(2.19)(3.12),利用矩阵
的对称正定性(注意,这里假设了正定性,而非半正定性),再结合矩阵范数的定义,可以得到如下结论
其中, 是矩阵A的条件数。条件数是一个不小于1的实数,它刻画了矩阵的数值稳定性,我在另一篇文章中介绍了条件数的由来,感兴趣的读者可前往阅读。在这里,我们无需理解条件数的意义,只要海森矩阵的条件数不是无穷大,
就一定不趋近于0,从而间接证明了
必然趋近于0。也就是说,牛顿法和拟牛顿法也必然会收敛。
证明完毕后,我们回归直觉。其实说了半天,无非是想说明最速下降法和两种牛顿法最终都会收敛。从直觉上来看这是自然而然的事情,只要选取的优化方向朝向梯度下降方向(即便有些许差异),每次迭代产生的少量进展终究会驱使函数到达极小值。但数学就是一个严肃的学科,看起来显然成立的命题也必须经过严格的证明。在上面的证明中,Lipschitz continuous性质和Wolfe conditions都是必不可少的,这也恰好说明了直觉和严格证明之间的差异,从直觉出发,我们是很难想到这两个约束条件的。
既然三种方法都能收敛,那谁收敛得更快呢?如果让我猜的话,我会猜牛顿法和拟牛顿法比最速下降法快,因为前两者计算优化方向时考虑了目标函数的二阶近似,应该比无脑沿着梯度下降方向走要好一些。但是否真的如此,或者快多少,就需要严格的数学证明了。
先来研究最速下降法的收敛速度,从一个简单的特例入手。对于下面这个多维变量二次函数,
假设 对称且正定(该条件模仿一维变量二次函数的二次项恒大于0的特性),我们其实可以直接求出它的极值点,令
即可,即线性方程
的解。
不过,现在要研究的是最速下降法,所以我们仍然按照最速下降法的求解步骤,看看会得到怎样的结果。最速下降法的搜索方向为梯度的反方向,即 ,那么在该方向上搜索一个最优的步长,相当于最小化
,带入式(3.24)的定义,令其导数等于0,可以解得最优的步长为
。这里需要提醒的一点是,由于我们假设了二次函数,所以才可能直接求出最优的步长,对于任意非线性函数,最优步长一般是无法求得解析解的,所以才会有上篇文章中提到的Backtracking Line Search方法。
求得的这个步长其实有很直观的物理意义,下图展示了优化过程中走过的路径。
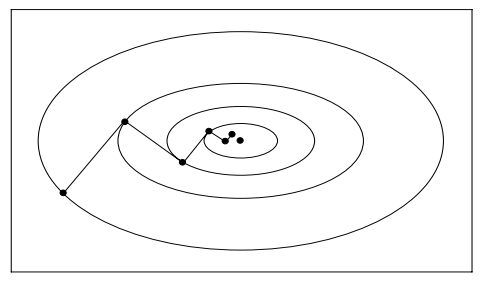
可以发现,每次迭代中求得的最优步长恰好是搜索线与目标函数的等高线的切点,因为整条搜索线上,该点的函数值最小。
回顾线搜索与信赖域中收敛速度的定义,里面涉及到向量之间的距离,或者说向量的范数。一般情况下,我们谈论的都是欧氏距离,即2范数。但在这里,为了方便证明,我们采用向量的Q范数,定义为 。在该定义下,考虑式(3.24),可以得到
这说明在Q范数意义上,当前点与极值点的距离等价于当前函数值与函数极值之差。然后经过一系列犀利的证明(此处省略一千字),可以得到下面的不等式
其中, 是
最小的特征值,
是
最大的特征值。对于正定矩阵来说,其特征值全部大于0且有限,所以
是个正常数,因此该式说明
线性收敛。
现在,我们证明了二次函数的最速下降法是线性收敛的。事实上,该收敛速度也可以推广到一般的非线性目标函数,但显然那是一个更复杂的证明了,我们暂时不去深究。
接下来,轮到牛顿法和拟牛顿法登场了,它们会不会具有超线性甚至二次收敛速度呢?
牛顿法的线搜索方向为 ,其中目标函数的二阶导
称为海森矩阵。前面提到过,海森矩阵具有半正定性质,这一性质有个缺陷,可能存在某些情况,使得
,这意味着
,即线搜索方向与梯度方向垂直,导致目标函数无法收敛。所以,我们一般考虑海森矩阵正定的情况,对于那些不正定的情况,后面的章节中会介绍一些手段将其变为正定。
我们的目标是推导 与
之间的关系,我们假设每次迭代的步长都为1,推导流程如下
其中,第4、6行利用了三角不等式。第5行将第4行的 写成积分形式
,并整理得到。第7行将与积分变量无关的
提到积分号外面,并假设目标函数的二阶导满足Lipschitz continuous,即
,再整理即可。第9行用到了一个显而易见的条件,当
时,
,于是有
。
最后的结果说明,当海森矩阵正定且Lipschitz continuous时,牛顿法二次收敛,且每次迭代的步长只需要恒定为1即可。
拟牛顿法是用矩阵 近似目标函数的二阶导海森矩阵,那就存在一个问题,什么样的近似才能算作合理的近似呢?毕竟,不可能任意的近似都具有相同的收敛速度。因此,我们规定,满足下面不等式的
才是对海森矩阵的合理近似
该式表明 在线搜索方向上逐渐逼近海森矩阵
,换句话说,
和
对线搜索的方向向量具有相同的变换效果。这里所谓的变换效果,就是把
变换到梯度下降方向
。
式(3.32)意味着分子是分母的高阶无穷小,于是有
其中,第2行左边加入的 是个常数,因为正定矩阵的范数一定有限,因此不影响等号左侧的无穷小阶数。同理,第3行也不影响无穷小的阶数。
接下来,从收敛速度的定义入手,即可推导出结果
其中,第4行的 来自于牛顿法中推导出的结果(3.37)。第5行用到了一个结论
,这一结论需要借助上式第4行的中间结果,利用三角不等式对
进行适当的放缩后得到,这里姑且省略。
从这一结果可以看出,拟牛顿法是超线性收敛的。由于 这一项的存在,且(3.32)规定了它只是
的无穷小,无法保证它是
的2阶无穷小,所以达不到牛顿法的收敛速度。
在结束本文前,我们再来看一个很有意思的线搜索方法——坐标下降法(Coordinate descent method)。它连目标函数的一阶导都不需要计算,直接轮流在各个坐标轴上搜索最优步长。比如,对于二维目标函数来说,它可能会走出下面这样的路线
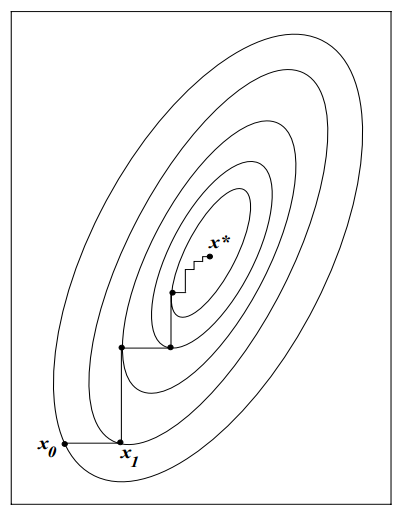
看起来还不错,哈?这种策略基于这样一个假设,在每个互相正交的方向上找到最优解,最终就能到达全局最优。直观上感觉是这样的,但实际上坐标下降法连最基本的收敛性都无法保证,即便能够收敛,也比最速下降法还要慢。
不过,仅凭不需要计算梯度这一点,坐标下降法就足以在优化算法中占据一席之地。
本文介绍了几种常用优化方法的收敛性和收敛速度。最速下降法、牛顿法和拟牛顿法都能收敛,收敛速度分别是线性、二次、超线性。坐标下降法不能保证收敛,但优点是不需要计算梯度。
矩阵的条件数 王金戈
怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的? 顾凌峰
上一篇:线搜索(一):步长的选取
下一篇:信赖域(一):Cauchy Point与Dogleg
原文:https://www.cnblogs.com/cx2016/p/13781699.html