给定一个可能具有重复数字的列表,返回其所有可能的子集。
在线评测地址:
样例 1:
输入:[0]
输出:
[
[],
[0]
]样例 2:
输入:[1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]解题思路
算法
举例分析
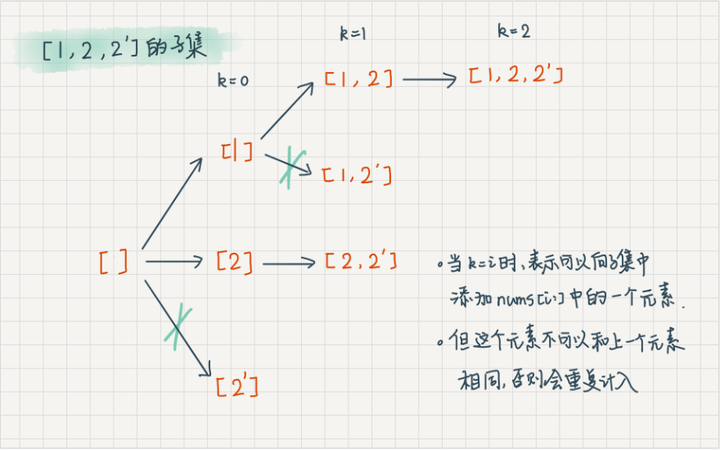
复杂度分析
代码
ublic class Solution {
/**
* @param nums: A set of numbers.
* @return: A list of lists. All valid subsets.
*/
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
// 排序
Arrays.sort(nums);
// dfs搜索
Deque<Integer> subset = new ArrayDeque<>(nums.length);
dfs(nums, 0, subset, res);
return res;
}
private void dfs(int[] nums, int k, Deque<Integer> subset, List<List<Integer>> res) {
// 当前组合存入res
res.add(new ArrayList<>(subset));
// 为subset新增一位元素
for (int i = k; i < nums.length; ++i) {
// 剪枝
if (i != k && nums[i] == nums[i - 1]){
continue;
}
subset.addLast(nums[i]);
// 下一层搜索
dfs(nums, i + 1, subset, res);
// 回溯
subset.removeLast();
}
}
}更多题解参考:
九章算法 - 帮助更多中国人找到好工作,硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧
【LeetCode/LintCode】Facebook面试题:子集 II
原文:https://www.cnblogs.com/lintcode/p/13707081.html