正交基
用 \(q_1、q_2、q_3...q_n\) 表示标准正交基,标准表示长度是单位长度,任何 \(q\) 都与其他 \(q\) 正交,她具有性质:
\[q_i^T.q_j=
\begin{array}{cc}
\{ &
\begin{array}{cc}
1 & i\neq j \ 0 & i=j \\end{array}
\\end{array}
\]
标准正交基让情况变好,她让整个计算方便很多,因为她们更容易操控,从不上溢和下溢出。
正交矩阵
我们把这些标准正交的向量放入矩阵 \(Q\) ,作为矩阵 \(Q\) 的每一列。
\[Q=\left(
\begin{array}{cccc}
q_1 & q_2 & ... & q_n \\end{array}
\right)
\]
前面我们已经研究过 \(A^TA\) ,我们再看看 \(Q^TQ\)
\[Q^TQ=\left(
\begin{array}{c}
q_1 \ q_2 \ ... \ q_n \\end{array}
\right).\left(
\begin{array}{cccc}
q_1 & q_2 & ... & q_n \\end{array}
\right)
=\left(
\begin{array}{cccc}
1 & 0 & ... & 0 \ 0 & 1 & ... & 0 \ ... & ... & ... & ... \ 0 & 0 & 0 & 1 \\end{array}
\right)=I
\]
结果为单位阵。
我们可以叫 \(Q\) 为标准正交矩阵。
作为惯例,当 \(Q\) 是方阵的时候,我们才叫她正交矩阵。
方阵的特点是,她具有逆矩阵,所以 \(Q^TQ=I\) ,说明 \(Q^T=Q^{-1}\) 。
举例1
\[perm Q=\left(
\begin{array}{ccc}
0 & 0 & 1 \ 1 & 0 & 0 \ 0 & 1 & 0 \\end{array}
\right)
\]
则 \(Q^TQ\) 为
\[\left(
\begin{array}{ccc}
0 & 1 & 0 \ 0 & 0 & 1 \ 1 & 0 & 0 \\end{array}
\right).\left(
\begin{array}{ccc}
0 & 0 & 1 \ 1 & 0 & 0 \ 0 & 1 & 0 \\end{array}
\right)=I
\]
举例2
\[Q=\left(
\begin{array}{cc}
\cos \theta & -\sin \theta \ \sin \theta & \cos \theta \\end{array}
\right)、Q=\frac{1}{\sqrt{2}}\left(
\begin{array}{cc}
1 & 1 \ 1 & -1 \\end{array}
\right)、Q=\frac{1}{2} \left(
\begin{array}{cccc}
1 & 1 & 1 & 1 \ 1 & -1 & 1 & -1 \ 1 & 1 & 1 & 1 \ 1 & -1 & 1 & -1 \\end{array}
\right)
\]
只有 \(1\) 和 \(-1\) 的正交矩阵称为阿德玛(Adhemar)矩阵。列向量长度为 \(1\) 才是单位向量,所以前面乘以相应的系数进行标准化。
举例3
\(Q\) 当然也可以是长方矩阵。
\[Q=\frac{1}{3} \left(
\begin{array}{ccc}
1 & -2 & 2 \ 2 & -1 & -2 \ 2 & 2 & 1 \\end{array}
\right)
\]
意义
重复一边,写 \(Q\) 就表示标准正交列向量的矩阵。
假设要投影到列空间中
\[\begin {align}
P&=Q(Q^TQ)^{-1}Q^T\&=QQ^T
\end {align}
\]
所以,标准正交矩阵简化了投影矩阵的计算。长方矩阵里面列向量是标准正交,相乘也为单位阵。
如果 \(Q\) 是方阵,则
\[\begin {align}
P&=QQ^T\&=I
\end {align}
\]
此时 \(Q\) 列空间就是整个空间,因为列向量方阵,\(m=n\),且是标准正交基,每列线性无关,她们的线性组合是整个空间,投影到整个空间的投影矩阵就是单位阵,矩阵 \(b\) 的每个向量还在原来的位置,不要改变。(注意,是方阵)
所有的复杂方程,在使用标准正交基后,都会变得非常简单。
正规方程(\(normal equation\))中:
\[\begin {align}
A^TA\hat x=A^T b
\end {align}
\]
变为 \(Q\) :
\[\begin {align}
Q^TQ\hat x&=Q^T b\\rightarrow I\hat x&=Q^T b
\end {align}
\]
这个方程表示,\(\hat x\) 的分量等于 \(Q^T\) 一行乘以 \(b\) ,即 \(\hat x\) 的 第 \(i\) 个分量等于第 \(i\) 个基向量乘以 \(b\) .
\[\hat x_i=q_i^T.b
\]
Graham-Schmidt正交化法
消元法的目的是将矩阵简化为三角矩阵。
而格拉姆-施密特(Graham-Schmidt)正交化法是将矩阵正交化,使列向量标准正交。
两列线性无关向量
从两列线性无关向量的情况开始
假设有有个向量 \(a、b\) ,我们想把这两个向量正交化得到标准正交向量 \(q_1、q_2\)
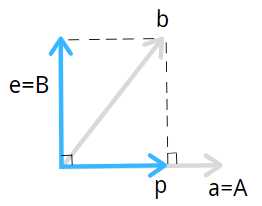
第一步:将任意两个线性无关向量转换为正交向量 \(A、B\)。
保持 \(a\) 方向不变,求与 $a $ 垂直的向量,即误差向量 \(e\) .故
\[\begin {align}
A&=a\B&=e\&=b-p\&=b-xa\&=b-\frac{ A^TA}{ A^Tb}A
\end {align}
\]
第二步:将正交向量 \(A、B\) 标准化
\[q_1=\frac{ A}{ ||A||}\q_2=\frac{ B}{ ||B||}\\]
这就是格拉姆-施密特(Graham-Schmidt)正交化法。
三列线性无关向量
假设有有个向量 \(a、b、c\) ,我们想把这两个向量正交化得到标准正交向量 \(q_1、q_2、q_3\) .
第一步:将任意三个线性无关向量转换为正交向量 \(A、B、C\)。
\(A、B\) 同两列线性无关向量一样,
\[\begin {align}
A&=a\B&=e\&=b-p\&=b-xa\&=b-\frac{ A^Tb}{ A^TA}A
\end {align}
\]
\(B\) 其实是向量 \(b\) 减去其在 \(a\) 方向上的投影。
所以 \(C\) 同时需要减去其在 \(a、b\) 方向上的投影,因为 \(C\) 应该同时垂直于 \(A、B\)。
\[C
=c-\frac{ A^Tc}{ A^TA}A-\frac{ B^Tc}{ B^TB}B
\]
第二步:将正交向量 \(A、B、C\) 标准化
\[q_1=\frac{ A}{ ||A||}\q_2=\frac{ B}{ ||B||}\q_3=\frac{ C}{ ||C||}\\]
举例
假设两个向量 \(a、b\)
\[a=\left(
\begin{array}{c}
1 \ 1 \ 1 \\end{array}
\right),b=\left(
\begin{array}{c}
1 \ 0 \ 2 \\end{array}
\right)
\]
我们对其标准正交化,得
\[A=\left(
\begin{array}{c}
\frac{1}{\sqrt{3}} \ \frac{1}{\sqrt{3}} \ \frac{1}{\sqrt{3}} \\end{array}
\right),B=\left(
\begin{array}{c}
1 \ 0 \ 2 \\end{array}
\right)-\frac{3}{3} \left(
\begin{array}{c}
1 \ 1 \ 1 \\end{array}
\right)=\left(
\begin{array}{c}
0 \ -1 \ 1 \\end{array}
\right)
\]
将她们放入矩阵 \(Q\) 中
\[Q=\left(
\begin{array}{cc}
\frac{1}{\sqrt{3}} & 0 \ \frac{1}{\sqrt{3}} & -1 \ \frac{1}{\sqrt{3}} & 1 \\end{array}
\right)
\]
假设原来的两个向量放入矩阵 \(D\) 中。
\[D=\left(
\begin{array}{cc}
1 & 1 \ 1 & 0 \ 1 & 2 \\end{array}
\right)
\]
\(D\) 和 \(Q\) 的列空间其实是一样的,都是同一个平面,因为 \(B\) 是 \(a、b\) 的线性组合,\(A\) 是 \(a\) 的线性组合。我们的计算只是让矩阵的基标准正交而已。
通过让矩阵的基标准正交,让投影以及其他的计算更加简单。
表达式
我们可以将格拉姆-施密特(Graham-Schmidt)正交化法用一个矩阵表示,即存在一个上三角矩阵 \(R\) ,使得
\[A=QR
\]
以 2列 矩阵 \(A\) 为例
\[\left(
\begin{array}{cc}
a_1 & a_2 \\end{array}
\right)=\left(
\begin{array}{cc}
q_1 & q_2 \\end{array}
\right).\left(
\begin{array}{cc}
a_1^T q_1 & a_2^T q_1\ a_1^T q_2& a_2^T q_2\\end{array}
\right)=\left(
\begin{array}{cc}
q_1 & q_2 \\end{array}
\right).\left(
\begin{array}{cc}
a_1^T q_1 & a_2^T q_1\ 0& a_2^T q_2\\end{array}
\right)
\]
\(a、q\) 都表示列向量。
其中,因为\(q_1\) 与 \(a_1\) 方向一样, \(q_2\) 与 \(a_1\) 正交 ,所以 \(a_1^Tq_2=0\),而 $ a_2^T$ 与 \(q_1\) 的夹角与 $ a_2$ 与 \(a_1\) 夹角一样,不是正交关系,所以不等于零。矩阵 \(R\) 是一个上三角矩阵。
格拉姆-施密特(Graham-Schmidt)将一组线性无关列的矩阵 \(A\) ,转换为一组标准正交列的矩阵 \(Q\),而两个矩阵的联系是一个上三角矩阵。
线性代数17.正交矩阵和格拉姆-施密特
原文:https://www.cnblogs.com/ckk-blog/p/13682300.html
