栈和队列是一种逻辑上的数据结构,栈,遵循先进后出的原则,在编译器中得到的应用较多,例如对于括号的匹配(这也是常见的算法题目),表达式的转换等,由于我们只关心栈顶元素,并不需要直接取到栈中间的元素,队列结构类似,只关心首尾元素,十分契合我们链表的特点,
而原本java中是存在stack类的,但现在已经不推荐使用了,一般将Deque这个接口当作栈来使用,它实现的是一个双端队列
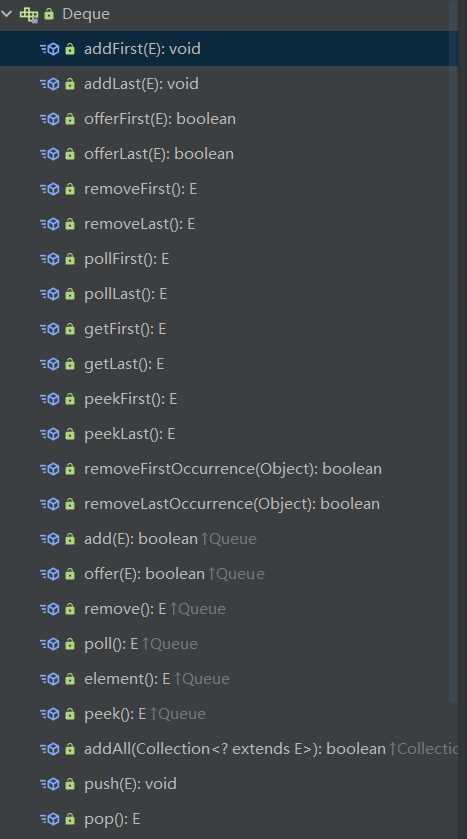
作为栈使用的时候一般就用,push(),pop(),peek() 几个方法
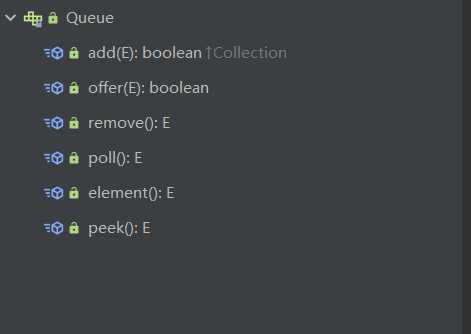
队列遵循先进先出的原则,一般用以作任务队列,Queue接口实现方法有:
堆是一棵完全二叉树,最小值总是存在于顶点处,
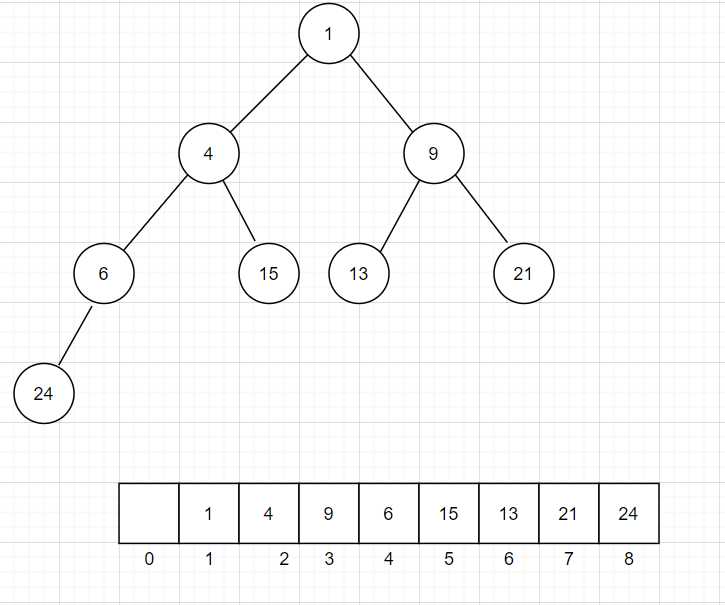
将这样一棵完全二叉树填入数组中,对于任意一个位置 i ,他的左子节点就在它的2*i 处,右子节点在2*i +1 处,父节点在 i/2 处,所以我们可以用队列来完成一个堆的结构。
当我们用堆进行一个添加操作时:
public boolean add(E e) {
return offer(e); // 使用了offer()方法
}
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1); // 对数组进行扩容
siftUp(i, e); // 将数据插入到合适的位置
size = i + 1;
return true;
}
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x, queue, comparator);
else
siftUpComparable(k, x, queue);
}
private static <T> void siftUpUsingComparator(
int k, T x, Object[] es, Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = es[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
es[k] = e;
k = parent;
}
es[k] = x;
}
private static <T> void siftUpComparable(int k, T x, Object[] es) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = es[parent];
if (key.compareTo((T) e) >= 0)
break;
es[k] = e;
k = parent;
}
es[k] = key;
}
插入策略是在末尾创建一个空位,然后将这个插入元素与父节点进行比较,满足条件就和父节点交换,直到退出循环;
删除根节点数据策略也类似,每次将左子节点和右子节点的最小数据放到父节点处即可(以小顶堆为例);
原文:https://www.cnblogs.com/xtoshii/p/13681819.html