拍集体照时队形很重要,这里对给定的 N 个人 K 排的队形设计排队规则如下:
每排人数为 /(向下取整),多出来的人全部站在最后一排;
后排所有人的个子都不比前排任何人矮;
每排中最高者站中间(中间位置为 /,其中 m 为该排人数,除法向下取整);
每排其他人以中间人为轴,按身高非增序,先右后左交替入队站在中间人的两侧(例如5人身高为190、188、186、175、170,则队形为175、188、190、186、170。这里假设你面对拍照者,所以你的左边是中间人的右边);
若多人身高相同,则按名字的字典序升序排列。这里保证无重名。
现给定一组拍照人,请编写程序输出他们的队形。
输入格式:
每个输入包含 1 个测试用例。每个测试用例第 1 行给出两个正整数 N(≤,总人数)和 K(≤,总排数)。随后 N 行,每行给出一个人的名字(不包含空格、长度不超过 8 个英文字母)和身高([30, 300] 区间内的整数)。
输出格式:
输出拍照的队形。即K排人名,其间以空格分隔,行末不得有多余空格。注意:假设你面对拍照者,后排的人输出在上方,前排输出在下方.
输入
Bob Tom Joe Nick Ann Mike Eva Tim Amy John输出
10 3 Tom 188 Mike 170 Eva 168 Tim 160 Joe 190 Ann 168 Bob 175 Nick 186 Amy 160 John 159
从简单开始想起:
首先排序。我这里是从小到大排。
由题目可以知道除了最后一排的每排人数为rs=N/K, 最后一排的个数为lastrs=N/K+N%(N/K)
这意味着 最后一排的对象在数组中的位置为 N-lastrs+1~N,
倒数第二排的对象在数组中的位置为 N-lastrs+1-rs~N-lastrs
倒数第n排的对象在数组中的位置为 N-lastrs+1-rs*(n-1)~N-lastrs-rs*(n-2)
现在我们已经得到了每行的数据都是啥,接下来就是给每行数据进行重排。
为了将题目简化,我们可以理解为对于某一行对象从l到r的重排, 对象个数为len=r-l+1
当len为奇数的时候:
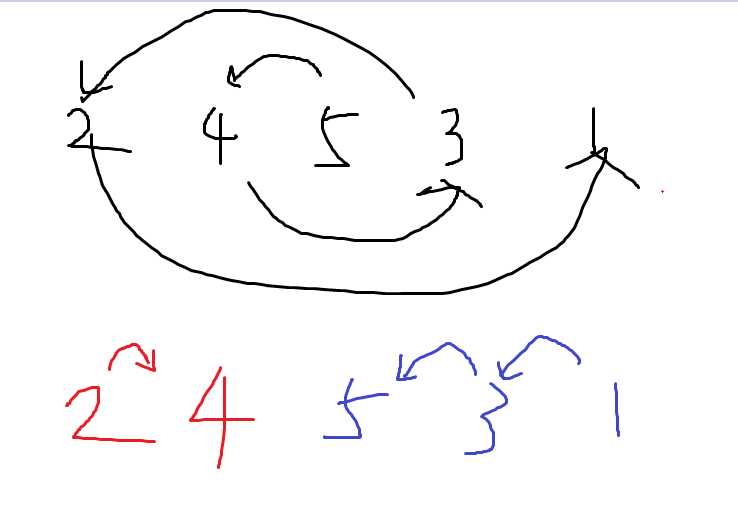
黑色笔迹的是题意的思路。从大到小插入,然后输出, 但是这样很不方便。
红色和蓝色笔迹是另一种思路。把每一次插入都计数num。当是奇数的时候往蓝色部分插入,当是偶数的时候往红色部分插入。输出的时候红色部分直接按照插入的顺序输出,蓝色部分需要倒序输出。
因此我们可以在num为偶数的时候读到红色部分就直接输出,num为奇数的时候存到一个栈里面,数据读完后弹出所有的内容。
当len为偶数时:
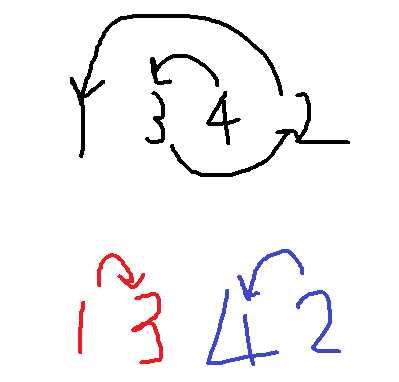
思路同上。但是红色部分变为当num为奇数,蓝色部分变为num为偶数。
代码
1 #include<iostream> 2 #include<cstring> 3 #include<fstream> 4 #include<algorithm> 5 #include<stack> 6 using namespace std; 7 typedef long long ll; 8 const ll mx=1e4+10; 9 typedef struct node{ 10 string name; 11 ll sg; 12 }STU; 13 STU stu[mx]; 14 bool cmp(const STU&a, const STU&b){ 15 if(a.sg==b.sg) return a.name>b.name; 16 return a.sg<b.sg; 17 } 18 void paidui(ll l, ll r){ 19 stack<string>q; 20 ll num=0, base=(r-l+1)%2==0?1:0;//len 偶数base为1 21 bool appe=false; 22 for(ll i=l;i<=r;i++){ 23 num++; 24 if(num%2==base){//红色部分 直接输出 25 if(appe) cout<<" "; 26 appe=true; 27 cout<<stu[i].name; 28 } 29 else{ 30 q.push(stu[i].name); 31 } 32 } 33 while(!q.empty()){//蓝色部分 栈弹出使其倒序输出 34 if(appe) cout<<" "; 35 cout<<q.top(); 36 q.pop(); 37 } 38 cout<<endl; 39 } 40 int main(){ 41 ll N, K; 42 cin>>N>>K; 43 for(ll i=1;i<=N;i++){ 44 cin>>stu[i].name>>stu[i].sg; 45 } 46 sort(stu+1, stu+N+1, cmp); 47 48 ll rs=N/K, lastrs=rs+N%rs; 49 //第一行 最后一排 50 ll d=N-lastrs+1; 51 paidui(d, N); 52 53 //其他几行 54 for(ll i=1;i<=K-1;i++){ 55 paidui(d-rs*i, d-1-rs*(i-1)); 56 } 57 58 return 0; 59 }
原文:https://www.cnblogs.com/sloth612/p/13653132.html