在介绍AdaBoost的时候我们讲到了,AdaBoost算法是模型为加法模型,损失函数为指数函数(针对分类为题),学习算法为前向分步算法时的分类问题。而GBDT算法是模型为加法模型,学习算法为前向分步算法,基函数为CART树(树是回归树),损失函数为平方损失函数的回归问题,为指数函数的分类问题和为一般损失函数的一般决策问题。在针对基学习器的不足上,AdaBoost算法是通过提升错分数据点的权重来定位模型的不足,而梯度提升算法是通过算梯度来定位模型的不足。
当GBDT的损失函数是平方损失(这需要回到损失函数类型,以及损失函数对应的优化问题上)时,即时,则负梯度
,而
即为我们所说的残差,而我们的GBDT的思想就是在每次迭代中拟合残差来学习一个弱学习器。而残差的方向即为我们全局最优的方向。但是当损失函数不为平方损失时,我们该如何拟合弱学习器呢?大牛Friedman提出使用损失函数负梯度的方向代替残差方向,我们称损失函数负梯度为伪残差。而伪残差的方向即为我们局部最优的方向。所以在GBDT中,当损失函数不为平方损失时,用每次迭代的局部最优方向代替全局最优方向(这种方法是不是很熟悉?)。
说了这么多,现在举个例子来看看GBDT是如何拟合残差来学习弱学习器的。我们可以证明,当损失函数为平方损失时,叶节点中使平方损失误差达到最小值的是叶节点中所有值的均值;而当损失函数为绝对值损失时,叶节点中使绝对损失误差达到最小值的是叶节点中所有值的中位数。相关证明将在最后的附录中给出。
训练集是4个人,A,B,C,D年龄分别是14,16,24,26。样本中有购物金额、上网时长、经常到百度知道提问等特征。提升树的过程如下:
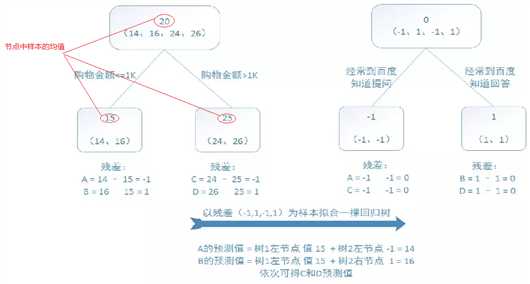
从上图可以看出,第一棵树建立的时候使用的是原始数据,而后每一棵树建立使用的是前n-1次的残差来拟合弱学习器。
下面,我们就来简单的介绍一下GBDT的基本原理和算法描述。
梯度提升算法的回归树基本模版,如下所示:
输入:训练数据集,损失函数为
输出:回归树
(1)初始化:(估计使损失函数极小化的常数值,它是只有一个根节点的树,一般平方损失函数为节点的均值,而绝对损失函数为节点样本的中位数)
(2)对(M表示迭代次数,即生成的弱学习器个数):
(a)对样本,计算损失函数的负梯度在当前模型的值将它作为残差的估计,对于平方损失函数为,它就是通常所说的残差;而对于一般损失函数,它就是残差的近似值(伪残差):
(b)对拟合一个回归树,得到第m棵树的叶节点区域
,
(J表示每棵树的叶节点个数)
(c)对,利用线性搜索,估计叶节点区域的值,使损失函数最小化,计算
(d)更新
(3)得到最终的回归树
原文:https://www.cnblogs.com/cgmcoding/p/13644213.html