在上述介绍中, nn.Module模块提供了网络骨架, nn.functional提供了各式各样的损失函数, 而Autograd又自动实现了求导与反向传播机制, 这时还缺少一个如何进行模型优化、 加速收敛的模块, nn.optim应运而生。
nn.optim中包含了各种常见的优化算法, 包括随机梯度下降算法SGD(Stochastic Gradient Descent, 随机梯度下降) 、 Adam(Adaptive Moment Estimation) 、 Adagrad、 RMSProp, 这里仅对常用的SGD与Adam两种算法进行详细介绍。
1. SGD方法
梯度下降(Gradient Descent) 是迭代法中的一种, 是指沿着梯度下降的方向求解极小值, 一般可用于求解最小二乘问题。 在深度学习中,当前更常用的是SGD算法, 以一个小批次(Mini Batch) 的数据为单位, 计算一个批次的梯度, 然后反向传播优化, 并更新参数。 SGD的表
达式如式(2-1) 与式(2-2) 所示
.

公式中, gt代表了参数的梯度, η代表了学习率(Learning Rate) ,即梯度影响参数更新的程度, 是训练中非常重要的一个超参数。 SGD优化算法的好处主要有两点:
·分担训练压力: 当前数据集通常数量较多, 尺度较大, 使用较大的数据同时训练显然不现实, SGD则提供了小批量训练并优化网络的方法, 有效分担了GPU等计算硬件的压力。
·加快收敛: 由于SGD一次只采用少量的数据, 这意味着会有更多次的梯度更新, 在某些数据集中, 其收敛速度会更快。
当然, SGD也有其自身的缺点:
·初始学习率难以确定: SGD算法依赖于一个较好的初始学习率,但设置初始学习率并不直观, 并且对于不同的任务, 其初始值也不固定。
·容易陷入局部最优: SGD虽然采用了小步快走的思想, 但是容易陷入局部的最优解, 难以跳出。
有效解决局部最优的通常做法是增加动量(momentum) , 其概念来自于物理学, 在此是指更新的时候一定程度上保留之前更新的方向,同时利用当前批次的梯度进行微调, 得到最终的梯度, 可以增加优化的稳定性, 降低陷入局部最优难以跳出的风险。 其函数如式(2-3) 与式(2-4) 所示。
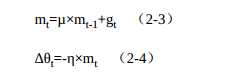
公式中的μ为动量因子, 当此次梯度下降方向与上次相同时, 梯度会变大, 也就会加速收敛。 当梯度方向不同时, 梯度会变小, 从而抑制梯度更新的震荡, 增加稳定性。 在训练的中后期, 梯度会在局部极小值周围震荡, 此时gt接近于0, 但动量的存在使得梯度更新并不是0, 从而有可能跳出局部最优解。
虽然SGD算法并不完美, 但在当今的深度学习算法中仍然取得了大量的应用, 使用SGD有时能够获得性能更佳的模型。
2. Adam方法
在SGD之外, Adam是另一个较为常见的优化算法。 Adam利用了梯度的一阶矩与二阶矩动态地估计调整每一个参数的学习率, 是一种学习率自适应算法。
Adam的优点在于, 经过调整后, 每一次迭代的学习率都在一个确定范围内, 使得参数更新更加平稳。 此外, Adam算法可以使模型更快收敛, 尤其适用于一些深层网络, 或者神经网络较为复杂的场景.
下面通过一个三层感知机的例子来介绍基本的优化过程。 新建一个mlp.py文件, 内容如下:

1 # from torch import optim 2 # optimizer = optim.SGD(model.parameters(), lr=0.001, momentum= 0.9) 3 # optimizer = optim.Adam([var1, var2], lr=0.0001) 4 5 import torch 6 from torch import nn 7 8 class MLP(nn.Module): 9 10 def __init__(self, in_dim, hid_dim1, hid_dim2, out_dim): 11 super(MLP, self).__init__() 12 13 self.layer = nn.Sequential( 14 nn.Linear(in_dim, hid_dim1), 15 nn.ReLU(), 16 nn.Linear(hid_dim1, hid_dim2), 17 nn.ReLU(), 18 nn.Linear(hid_dim2, out_dim), 19 nn.ReLU(0) 20 ) 21 22 def forward(self, x): 23 x = self.layer(x) 24 return x

1 import torch 2 from mlp import MLP 3 from torch import optim 4 from torch import nn 5 6 # 实例化模型, 并赋予每一层的维度 7 model = MLP(28*28, 300, 200, 10) 8 # 打印model的结构, 由3个全连接层组成 9 print(model) 10 >> MLP( 11 (layer): Sequential( 12 (0): Linear(in_features=784, out_features=300, bias=True) 13 (1): ReLU() 14 (2): Linear(in_features=300, out_features=200, bias=True) 15 (3): ReLU() 16 (4): Linear(in_features=200, out_features=10, bias=True) 17 (5): ReLU() 18 ) 19 ) 20 21 #采用SGD优化器, 学习率为0.01 22 optimizer = optim.SGD(params = model.parameters(), lr=0.01) 23 data = torch.randn(10, 28*28) 24 output = model(data) 25 26 # 由于是10分类, 因此label元素从0到9, 一共10个样本 27 label = torch.Tensor([1, 0, 4, 7, 9, 3, 4, 5, 3, 2]).long() 28 print(label) 29 >> tensor([1, 0, 4, 7, 9, 3, 4, 5, 3, 2]) 30 31 # 求损失 32 criterion = nn.CrossEntropyLoss() 33 loss = criterion(output, label) 34 print(loss) 35 tensor(2.2808, grad_fn=<NllLossBackward>) 36 37 # 清空梯度, 在每次优化前都需要进行此操作 38 o = optimizer.zero_grad() 39 40 # 损失的反向传播 41 l = loss.backward() 42 43 # 利用优化器进行梯度更新 44 ol = optimizer.step()
对于训练过程中的学习率调整, 需要注意以下两点:
·不同参数层分配不同的学习率: 优化器也可以很方便地实现将不同的网络层分配成不同的学习率, 即对于特殊的层单独赋予学习率, 其余的保持默认的整体学习率, 具体示例如下:

1 # 对于model中需要单独赋予学习率的层, 如special层, 则使用‘lr‘关键字单独赋予 2 optimizer = optim.SGD( 3 [{‘params‘: model.special.parameters(), ‘lr‘: 0.001}, 4 {‘params‘: model.base.parameters()}, lr=0.0001)
学习率动态调整: 对于训练过程中动态的调整学习率, 可以在迭代次数超过一定值后, 重新赋予optim优化器新的学习率。
原文:https://www.cnblogs.com/zhaopengpeng/p/13641309.html