网络流问题

1.什么是网络流

• 每一条路上都有最大可以承载的货物量，求单位时间内运送数量最大的

2.关于相关的定义

• 网络流图：没有自环的有向连通图
• 只有一个入度为0的点s，为源，一个出度为0的点T，为汇
• 每条边有一个非负的权值容量c（i,j），不能超过最大的流量

3.容许流

• 对于每条边e给定实数fe为边的流量、
• 需要满足：
• 1.每条边的流量小于容量 fe<ce
• 2.每个店的入流量=出流量 Σ(e=(x,i) fe = Σ(e(i,x) fe
• 3.圆点流出要等于汇点流入 W=Σe=(S,i) fe= Σe=(i,T) fe
• 则这个W就是容许流
• 我们希望这个容许流是最大的（求最大流）

4.最大流算法、

• 有流量为0的容许流开始，然后在其中增加流量，（虚招增广路）
• 称为增广过程

5.简单算法

4.关于FF算法：

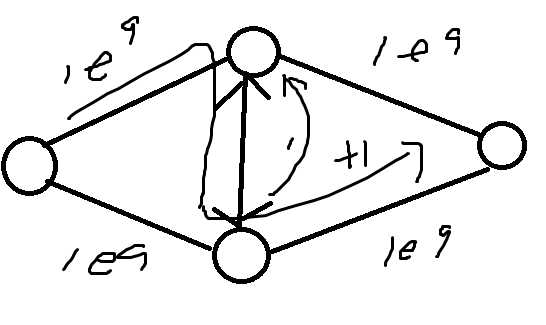
EK算法：每次找最短的一条增广路来增广，（BFS实现）O（m^2n）

每次求完之后，最短路的长度是一直在变大的

 分层图：通过bfs求出每个点的最短路径disi则只考律disv==disu+1 的e(u,v)

时间复杂度：O(n^2m)O(n2m)，一般能够处理10^4104~10^5105规模的网络

相较于EKEK算法，显然DinicDinic算法的效率更优也更快：虽然在稀疏图中区别不明显，但在稠密图中DinicDinic的优势便凸显出来了（所以DinicDinic算法用的更多）

 6.最大流最小割定理：

• 割切储存的是(S,S-)时间的由S点集到S补集点集中间的所有边sou属于S，des属于S-，割就是中间这些边的流量之和
• 也就是说，割实际上从图中选出若干条边，是的sou到达不了des
• 因为任意流一定要经过割，所以任意流小于任意割
• 在残量网络中，将sou能够到达的点放在V，不能的点放在V-里面，所以所有的割都是满流的（否则V,V-就会发生变化）那么割切就是最大流的流量
• 如果最大流某一个的流量对应的割，那么他就是最小的割了（因为最大流已经流满了）
• 求出最大流的时候观察dis集合我们就可以得到最小割

 7.建模;

• 我们一般转化为最小割问题，用最大流算法求解
• 关键点并不是在算法，而是在于我们应该怎么样子连边建图使这道题目转化为一到网络流问题

8.经典模型：网络流24题

• 二分图匹配问题（飞行员匹配）：匈牙利算法，网络流,O（n根号m）
• 基本技巧1：建立超级源点和超级汇点，由这两点连出的边表示选择的方案数

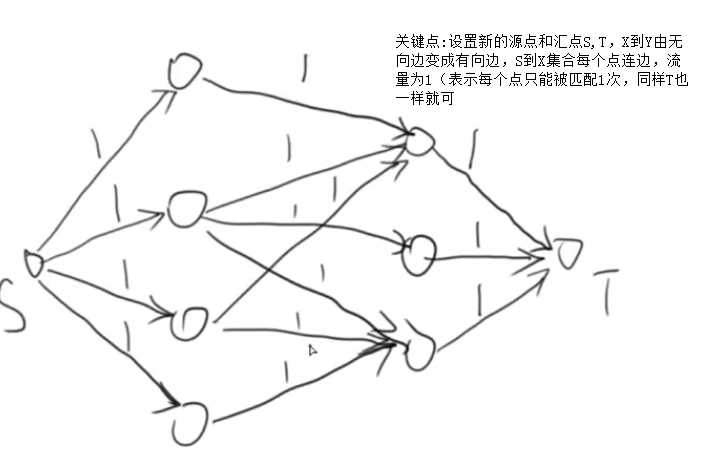
• 2.圆桌问题：
• 技巧2：二分图模型中间点的容量表示可以对应几次（一个单位的代表对应一个餐桌只能一次）
• 

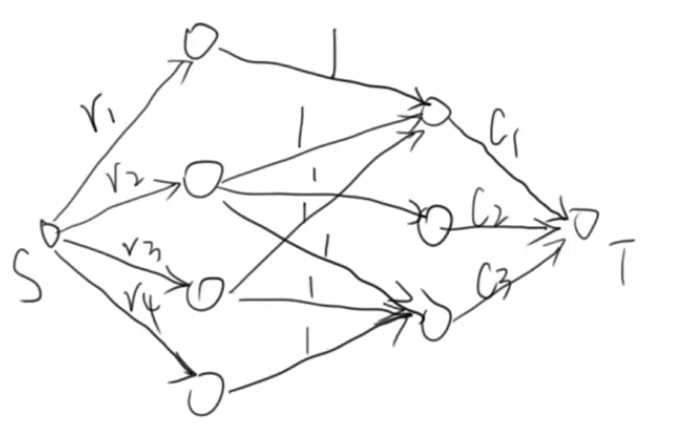
   3.最小路径覆盖问题;

• 简单路径：路径中没有重复的点（每一个点的入度和出度最多为1 1）
• 

• 技巧四：建立对应点：（什么意思，我们发现一条最短路径对应的两个属性（入度和出度），所以就是我们需要流进一个点和流出一个点来，所以我们需要对一个点同时进行流入和流出两种操作，所以说我们需要建立对应点）拆点技巧
• 技巧五：思考二分图模型匹配后和未匹配的所附加的意义（这也是本题中思考的最重要的一个技巧）

4.魔术球问题

现在我们可以对题目进行一下抽象：

1.只能在柱子上面放球（连边的顺序：有向边）

2.两边之和为平方数：满足关系才可能连边（同样这一个条件也在暗示这是一条简单路径：只有相邻两个点满足性质，并且它的开头永远不会相撞【注意底端了啊】）

3.求n根柱子最多可以满足多少个球（或者求多少个求对应的柱子最大为n）【转求解变为比较验证】

•  本题考查逆向思维（就如同质因数和n的关系一样）
• 思考方式：逆向求证（证明题一般是比求解题是好做的）【基本套路：如果说题目所求答案根据我们的条件是单调的，我们可以通过增加答案数来求取条件，直到条件符合，那么这就是答案】
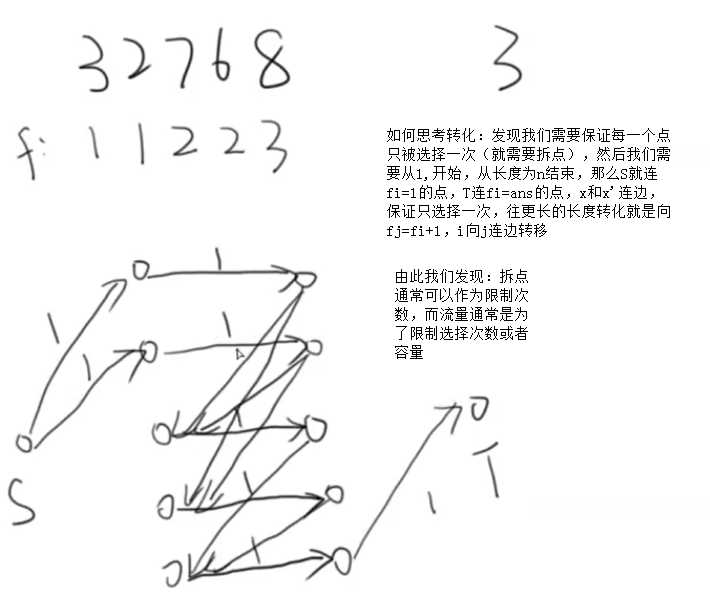
• 根据球进入的顺序，我们直到i到j的话，j>I的话j是在后边进入，如果说i+j是完全平方，就连上一条边就可以了
• 最后就是求最大路径覆盖数，也就是n满足时对应的球的个数
• 最大流算法的特殊性：他是一个增广算法，也就是说，就算wangle图里面新家边和边权，原来的最大流一样是可行的

5.最长上升子序列模型

•  如果是选择任意次,相当于把容量改成无限就好

 6.方格取数问题;

大意：在nxm的格子当中取数，且取出的数之间没有公共边，求最大的数的数量

• 发现了，这是一个相互矛盾的集合，（求出来一个另一个就不行），所以我们考虑染色
• 染色方法：编号和为奇数编在一起，偶数编在一起
• 引入两个问题：

• 如何取出方案呢：我们跑了一遍最大流之后再剩余的残量网络当中，将S可以到达的点集归为V，不能到达的点集归为V-那么由此我们就知道了V和V-的那些边被割掉

7.太空旅行模型

• 闭合图：每个点的出边仍指向图内（是原图的一个部分）使得每个点的后继都在子图里面，这个子图就叫最大权闭合子图。 
• 最大权闭合图模型：抽象出来，（选择一部分之后，另一部分必须选择），那么相当于这就是一个最大权闭合图模型：
• 在物理意义上就是事物之间关系的依赖性，一个事件发生前其他事件必须发生
• 也就是说，我们可以将边和点都看作事件，边事件的发生依赖于两个点事件的发生
• 小结一下：在任意带权有向图当中，只要是有依赖性质的条件，最大权闭合图模型是普惠性的算法
• 本题是二分图：左边是实验，右边是仪器，左边是正权，右边是负权，必须是闭合图才可以
• 技巧六：当我们将中间边容量设置为正无穷时：正面看，这个点会被选择无限多次。反面看：再最小割问题中，这个边一定是不会被割掉的
• 

   

   

•  

   

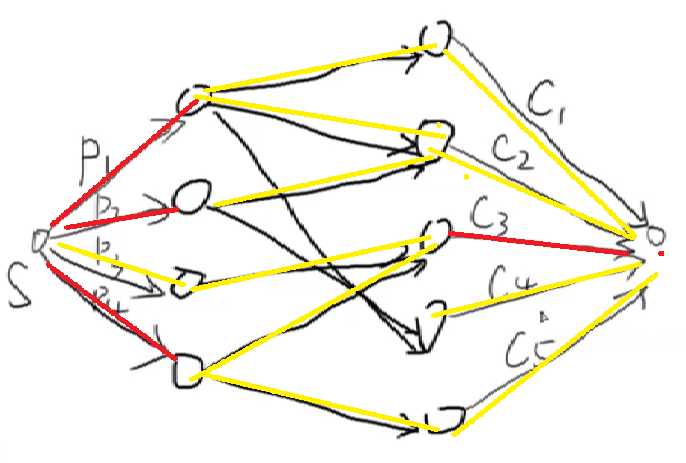
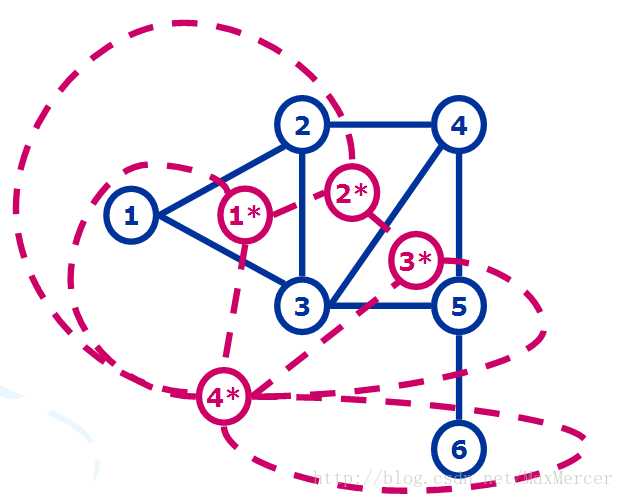
  在图中我们给出一个相应的解释：

• 如图，我们知道最大权闭合图是V|S，也就是P3；

• 割掉S和I的边，表示I不进如子图当中，如果割掉I和T的边，那么表示I进入子图当中，所以本题中(P3和C3)进入了最后的子图当中
• 那么这个样子的话，我们就得到了如下的证明：

• 合法性

  只有s与t不连通时，才能得到闭合子图。

  如果s与t连通，则存在点i,j，使得s到i有边，i到j连通，j到t有边，所以j一定是i的后继，但选择了i，没有选择j，不是闭合子图。（根据上面割掉和没有割掉的定义来解释）

  如果s与t不连通，选择了正权点i，一定选择了i后继中的所有负权点。设j是i的后继中的正权点，则割掉s到j的边是没有意义的，最小割不会割掉它，则j一点被选中，所以i的所有后继都被选中，符合闭合图的定义。

  最优性

  最小割=(不选的正权之和+要选的负权绝对值之和） 
  最大权闭合子图=（正权之和-不选的正权之和-要选的负权绝对值之和）=正权值和-最小割 
  因为正权值和，是定值，而最小割保证值最小，所以最大权闭合子图一定最优

• 那后这里补充一个关于最大权闭合图模型的改进和优化http://www.360doc.com/content/18/0918/19/48548007_787750583.shtml（POLYA）
• https://wenku.baidu.com/view/f11c5f8dd15abe23482f4df4.html（模型改进）

省选题啦：

• SCOI2007 蜥蜴：
• 通过拆点，来控制经过一个点的次数
• 所以说把一个点拆成两个，相互之间容量为高度h(也就是只能条h次），S到原来有蜥蜴的石柱连边（需要几条可行流），转移的石柱之间，石柱跳出的容量为INF

切糕：

• 技巧七：网络流不局限于二分图，且网络流所对应的原图中的点权模型实际上是边上的数值（就比如本题）：
• 考虑到限制（在网络流图中限制要么使用容量来限制，要么就是通过割边来限制）我们发现每一个(x,y)都至少要去一个切割点，那么久将S,T中间连上z割节点（节点中间的边就是对应的权值w）
• 再考虑限制，我们发现：
• 

   

   

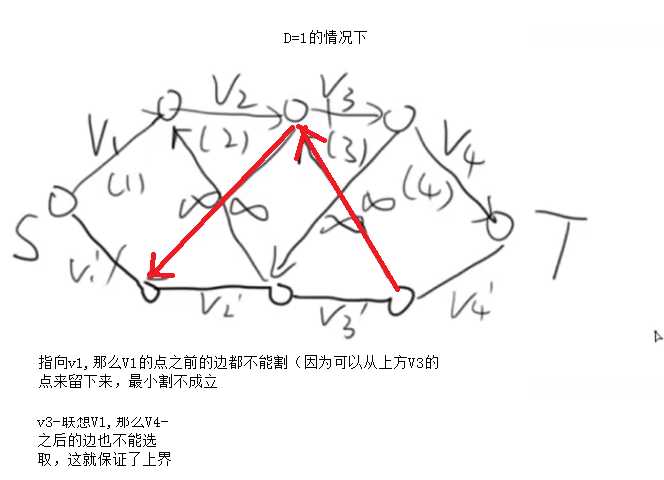
•  由此，我们给出一个解释：对于多个序列，其中智能选择一个或者n个流过的时候，我们通常将序列和ST联通，并且用割的形式来限制范围，为了防止限制边被割掉，容量设置为正无穷

狼爪兔子

• 对偶图最短路：
• 平面图：边只在点处相交的图
• 我们将由边切割成的面作为对偶图的点，原图G中的每一条边如果分割两个面，在G‘’中两个对应点连线，如果G中边两边都是同一个面，那么就给自己连一条回路
• 对G‘求解最短路，就是对原图求解最大流最小割；

   

   这个时候，因为原图的复杂度（比如n,m1000）这种数据就非常棒了

四.费用流

• 求出的费用流：费用是c*f（流过越大，费用越大）
• 最小费用最大流问题
• 费用和最小的路径是比较少的，所以用DINIC并不能优化多少
• 同时，对于反向边，费用取相反数，存在负权边，然后用SPFA就可

T1 晨跑

• 技巧八：如何表示一个点只经过一次：拆点，容量为1就可以：
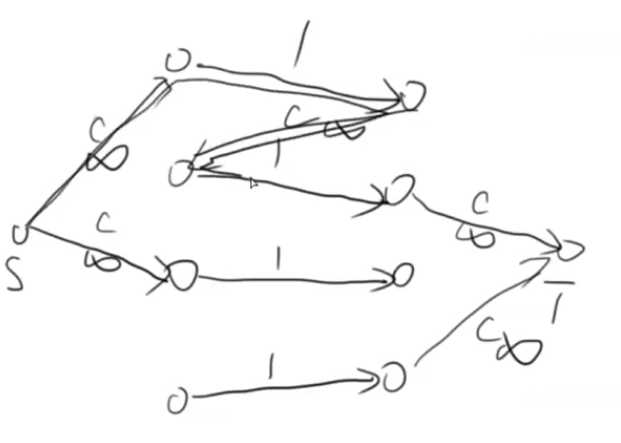• ：电和点之间的转化是没有限制的，就是流量没有限制，但是他们的c只能有一个

•  

  维护一个点只能走一次，c自然就是0

• 最小费用：存成负数不就是最大的值了吗

• 

   

   

   

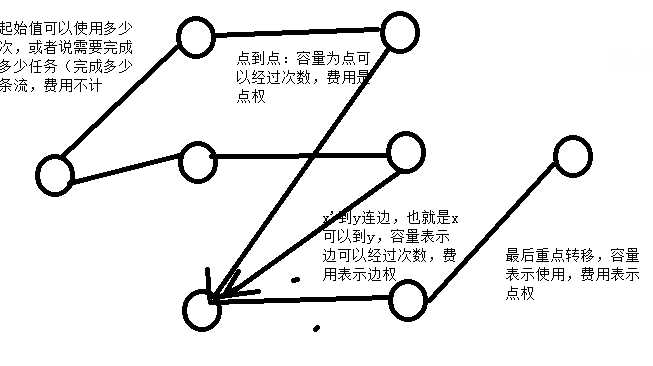
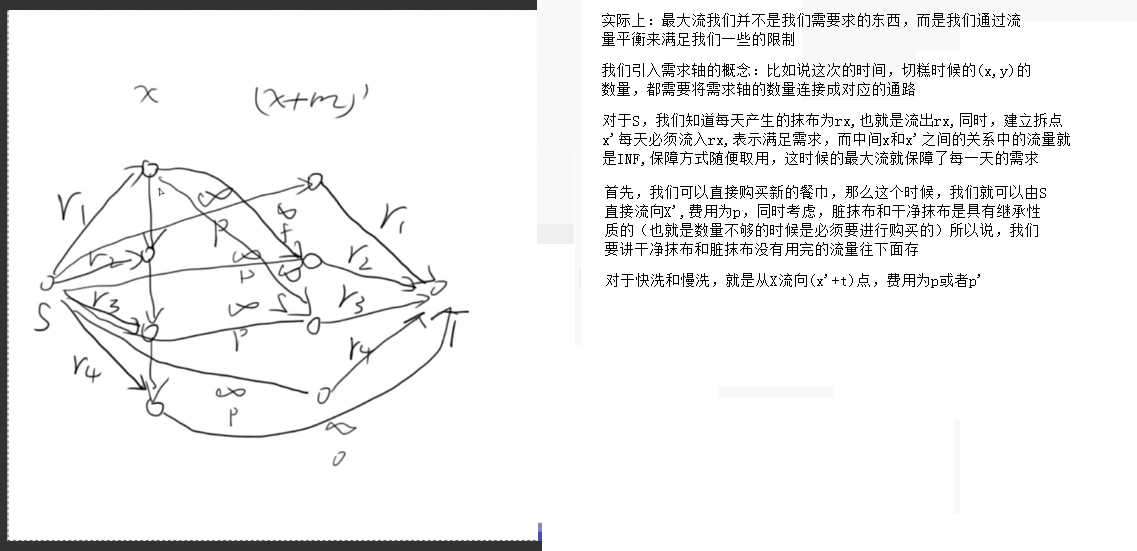
• 餐巾计划问题
• 这一次就出现了时间线这一个维度了
• 
• 营救皮卡丘：
• 如果说我们已经知道了破坏的顺序，那么距离是可以预处理的（因为只能通过先前的那些点）f[i][j]：从i，只经过(1-j)的最小距离（floyd）
• 重点关于利用流量来完成题目限制的重要因素：流量覆盖
•  对于0号点我们特殊处理，容量为k，费用为0就可

网络流问题

原文：https://www.cnblogs.com/ILHYJ/p/13601235.html